2021年秋季AMC10A第1-20题解析

点击领取>>>迎春杯、数学花园探秘真题、北青研学营、华杯杯赛、华数之星、走美杯、希望杯、美国杯赛大联盟真题

[Q1]What is the value of

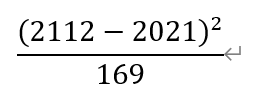
A)7    B)21    C)49    D)64    E)91

[答案]C

[解析]由已知得，

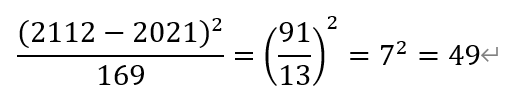
故选C。

[Q2]Menkara has a 4x6 index card. If she shortens thelength of one side of this card by 1 inch, the card would have area 18 squareinches. What would the area of the card be in square inches if instead sheshortens the length of the other side by 1 inch?

A)16    B)17    C)18    D)19    E)20

[答案]E

[解析]4x6的矩形，一条边减少1英寸，变为3x6，面积恰好为18平方英寸。另外一条边减少1英寸，变为4x5，面积应为20平方英寸。故选E。

[Q3]What is maximum number if balls of clay with radius 2that can completely fit inside a cube of side length 6 assuming that the ballscan be reshaped but not compressed before they are packed in the cube?

A)3    B)4    C)5    D)6    E)7

[答案]D

[解析]题目中要求半径为2的粘土小球可以塑形，但是不能压缩，所以体积不变。因此，只需要计算正方体和小球的体积比即可，

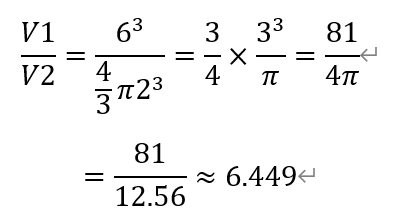
即体积比大于6，故选D。

或者采用估算，

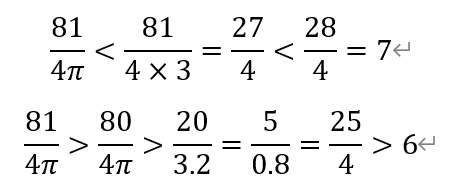
[Q4]Mr. Lopez has a choice of two routes to get to work.Route A is 6 miles long, and his average speed along this route is 30 miles perhour. Route B is 5 miles long, and his average speed along this route is 40miles per hour, except for a 1/2-mile stretch in a school zone where hisaverage speed is 20 miles per hour. By how many minutes is Route B quicker thanRoute A?

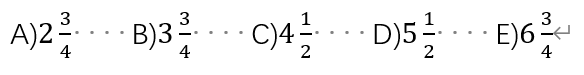
[答案]B

[解析]路线A花费的时间tb为，

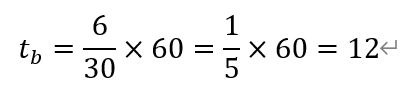
路线B花费的时间ta为，

因此，路线B比路线A用时少了，

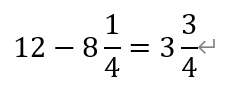
故选B。

[Q5]The six-digit number

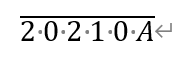
is prime for only one digit A. What is A?

A1    B)3    C)5    D)7    E)9

[答案]E

[解析]由于2+0+2+1+0+A=5+A，所以若该数为质数，则A除了是奇数以外，还不能是1、7，否则能被3整除；其次A还不能是5，否则能被5整除。

然后三位截断求差，有

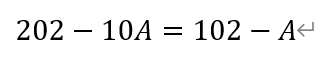
若A为3，则该差为102-3=99，能被11整除。

若A为9，则该差为102-9=93。因此A只能为9，故选E。

[Q6]Elmer the emu takes 44 equal strides to walk betweenconsecutive telephone poles on a rural road. Oscar the ostrich can cover thesame distance in 12 equal leaps. The telephone poles are evenly spaced, and the41st pole along this road is exactly one mile (5280 feet) from the first pole.How much longer, in feet, is Oscar’s leap than Elmer’s stride?

A)6    B)8    C)10    D)11    E)15

[答案]B

[解析]从第1根电话杆到第41根电话竿，共有40个间隔。这40个间隔的长度为1英里，即5280英尺。因此相邻两根电话杆之间的距离为：5280/40=132英尺。

于是，奥斯卡的步幅比埃尔默的步幅大，

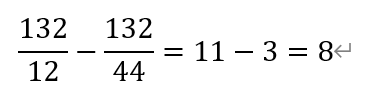
即8英尺。故选B。

[Q7]As shown in the figure below, point E lies in theopposite half-plane determined by line CD from point A so that ∠CDE=110°. Point F lies on AD so that DE = DF, and ABCD is a square. What isthe degree measure of ∠AFE?

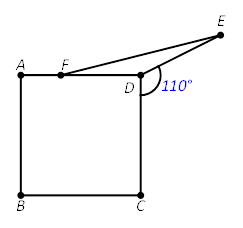
A)160    B)164    C)166    D)170    E)174

[答案]D

[解析]由已知得，

△EDF为等腰三角形，所以，

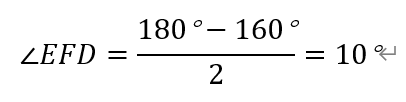
从而∠AFE=180°-10°=170°。故选D。

[Q8]A two-digit positive integer is said to be cuddlyif it is equal to the sum of its nonzero tens digit and the square of its unitsdigit. How many two-digit positive integers are cuddly?

A)0    B)1    C)2    D)3    E)4

[答案]B

[解析]设这个两位数的十位数字为x，个位数字为y,其中x≠0。则有，

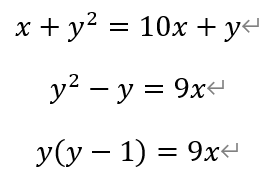
即y和y-1的乘积要能被9整除。

于是，要么y能被9整除，要么y-1能被9整除。若y-1=9，则y=10，不满足题意。因此只能是y=9，从而x=8，即这个数为89。

故选B。

[Q9]When a certain unfair die is rolled, and even numberis 3 times as likely to appear as an odd number. The die is rolled twice. Whatis the probability that the sum of the numbers rolled is even?

A)3/8    B)4/9    C)5/9    D)9/16    E)5/8

[答案]E

[解析]投掷一次，出现偶数的概率为3/4，出现奇数的概率为1/4。

投掷两次后，两次的点数之和为偶数，要么两次都是偶数，要么两次都是奇数，总的概率为，

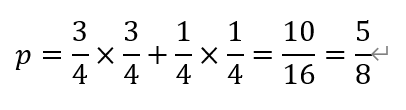
故选E。

[Q10]A school has 100 students and 5 teachers. In thefirst period, each student is taking one class, and each teacher it teachingone class. The enrollments in the classed are 50, 20, 20, 5, and 5. Let tbe the average value obtained if a teacher is picked at random and the numberof students in their class is noted. Let s be the average value obtainedif a student is picked at random and the number of students in their class,including that student, is noted. What is t-s?

A)-18.5    B)-13.5    C)0    D)13.5   E)18.5

[答案]B

[解析]根据题意，t是教师对应班级的学生人数的平均值，

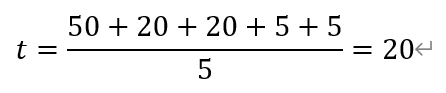
每个学生所对应班级人数的概率分布列为，

S是学生对应班级的学生人数的平均值，

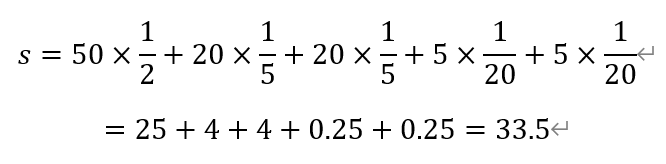
于是，s-t=20-33.5=-13.5。故选B。

[Q11]Emily sees a ship traveling at a constant speedalong a straight section of a river. She walks parallel to the riverbank at auniform rate faster than the ship. She counts 210 equal steps walking from theback of the ship to the front. Walking in the opposite direction, she counts 42steps of the same size from the front of the ship to the back. In terms ofEmily’s equal steps, what is the length of the ship?

A)70    B)84    C)98    D)105    E)126

[答案]A

[解析]设船的速度为v1，艾米莉的速度为v2。根据题意，有

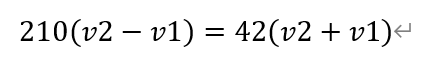
解得，

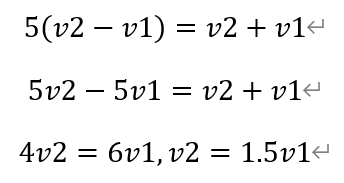
即艾米莉的速度是船的1.5倍。

从而船的全长为，

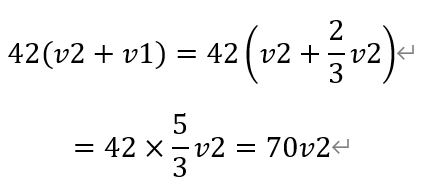
即艾米莉在静止情况下，走完船的全长需要70步。故选A。

[Q12]The base-mine representation of the number Nis 27,006,000,052_nine. What is the remainder when N isdivided by 5?

A)0    B)1    C)2    D)3    E)4

[答案]D

[解析]考虑9的n次方除以5的余数，分别为：

根据余数定理，可知该九进制数除以5的余数为：

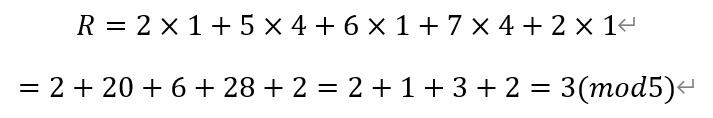
即值为3。故选D。

[Q13]Each of 6 ball is randomly and independently paintedeither black or white with equal probability. What is the probability thatevery ball is different in color from more than half of the other 5 balls?

A)1/64    B)1/6    C)1/4    D)5/16    E)1/2

[答案]D

[解析]根据题意，每个球的颜色都与其他5个球中半数以上球的颜色不同。显然只能是3个黑球和3个白球，任意取出一个球后，都会导致另外一种颜色占据多数。

不失一般性，设球的颜色为黑色为事件X。6个球中，取得3个黑球和3个白球的概率为，

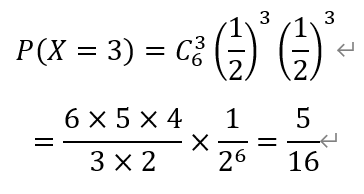
值为5/16。故选D。

[Q14]How many ordered pairs (x, y) of real numberssatisfy the following system of equations?

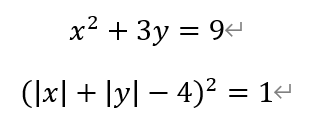
A)1    B)2    C)3    D)5    E)7

[答案]D

[解析]首先考虑点在坐标轴上的情况。根据第一个方程，当x=0时，y=3；当y=0时，x=±3。将(0,3)以及(3,0)和(-3,0)代入第二个方程，均满足等式。因此它们都是满足条件的解。

然后考虑点不在坐标轴上的情况。根据第二个方程，两边开方有，

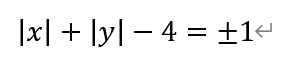
若x＞0，y＞0，则有

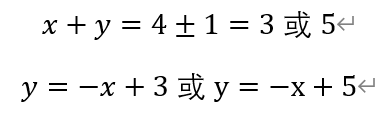
若x＞0，y＜0，则有

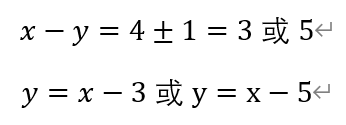
若x＜0，y＞0，则有

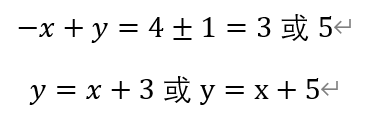
若x＜0，y＜0，则有

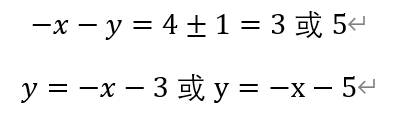
其中，只有下面两组解，

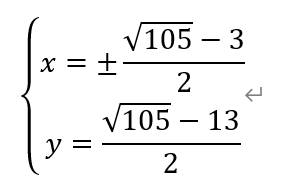
因此，原方程组共有五组解。故选D。

[Q15]Isosceles triangle ABC has AB = AC = 3√6,and a circle with radius 5√2 is tangent to line AB at Band to line AC at C. What is the area of the circle that passes throughvertices A, B, and C?

A)24π    B)25π    C)26π   D)27π    E)28π

[答案]C

[解析]设与△ABC中AB和AC相切圆的圆心为O。连接BO、CO和AO，如图所示。

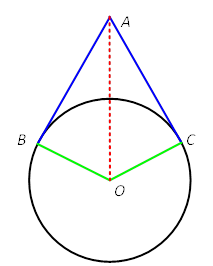
由于AB和AC为圆O的切线，所以AB⊥BO，AC⊥CO。在Rt△ABO或者Rt△ACO中，

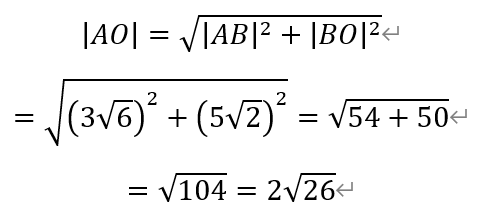
又由于∠ABO=∠ACO=90°，所以点A、B、O、C四点共圆，且以AO为直径。因此该圆的半径为√26，相应的面积为26π。故选C。

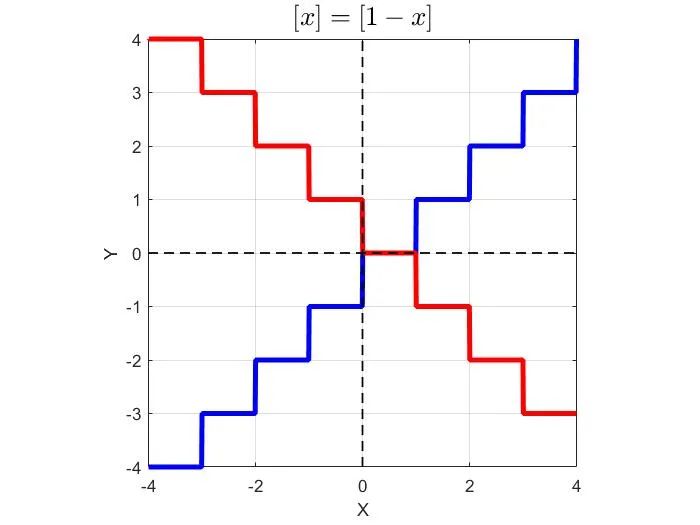
[Q16] The graph of

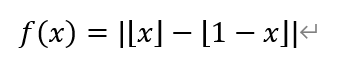
is symmetric about which of the following? (Here [x] is thegreatest integer not exceeding x.)

A)the y-axis    B)the line x = 1    C)theorigin 

D)the point (1/2,0)    E)the point (1,0)

[答案]D

[解析]由于函数f(x)带有绝对值，所以它是关于点对称。令f(x)=0，得

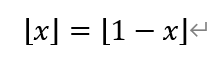
根据题意可知，[x]是向下取整，即地板函数。做出它们的图像可知，它们在[0,1]上都等于0，对称中心在(1/2,0)处。故选D。

[Q17]An architect is building a structure that will placevertical pillars at the vertices of regular hexagon ABCDEF, which is lyinghorizontally on the ground. The six pillars will hold up a flat solar panelthat will not be parallel to the ground. The heights of the pillars at A, B,and C are 12, 9, and 10 meters, respectively. What is the height, in meters, ofthe pillar at E?

A)9    B)6√3    C)8√3    D)17    E)12√3

[答案]D

[解析]延长BC和ED，交于点G，如图所示。

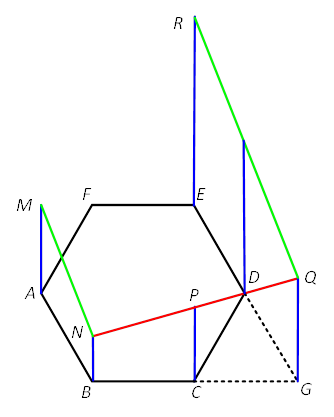
假设在点G也放置支柱，则太阳能电池板应位于平面MNPQR上。四边形BNQG和四边形ERQG为梯形，从而QE的长度应为：

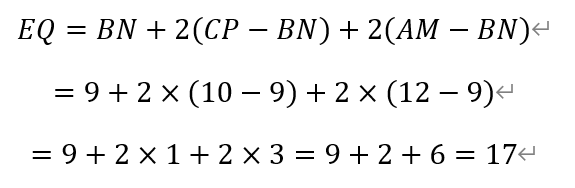
即值为17米。故选D。

[Q18]A farmer’s rectangular field is partitioned into a 2by 2 grid of 4 rectangular section as shown in the figure. In each section thefarmer will plant one crop: corn, wheat, soybeans, or potatoes. The farmer doesnot want to grow corn and wheat in any two sections that share a border, andthe farmer does not want to grow soybeans and potatoes in any two section thatshare a border. Given these restrictions, in how many ways can the farmerchoose crops to plant in each of the four sections of the field?

A)12    B)64    C)84    D)90    E)144

[答案]C

[解析]根据题意，玉米(C)和小麦(W)必须分开种植，大豆(S)和土豆(P)也要分开种植。如果恰好种植一种作物，方法数为4；

如果恰好种植两种作物，从四种作物中选出两种，有C₄²=6种情况。它们分别是：CW，CS，CP，WS，WP和SP。如果是CW和SP组合，每种组合有两种种植方法，如图所示。

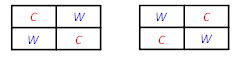
如果是CS，CP，WS，WP组合，每种组合有2⁴-4=14种种植方法，如图所示。

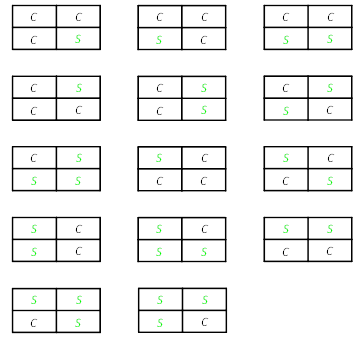
因此，恰好种植两种作物的方法数为：2×2+4×14=4+56=60种。

如果恰好种植三种作物，从四种作物中选出三种，有四种组合。每种组合都有4种种植方法，如图所示。 

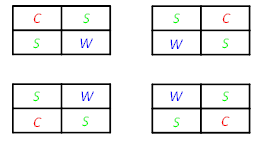
因此，恰好种植三种作物的方法数为：4×4=16种。

如果恰好种植四种作物，则共有2×2=4种种植方法。

综上，总的种植方法数为：4+60+16+4=84。故选C。

[Q19]A disk of radius 1 rolls all the way around theinside of a square of side length s ＞ 4 and sweeps out aregion of area A. A second disk of radius 1 rolls all the way around theoutside of the same square and sweeps out a region of area 2A. The value of scan be written as a + bπ/c, where a, b,and c are positive integers and b and c are relativelyprime. What is a+b+c?

A)10    B)11    C)12    D)13    E)14

[答案]A

[解析]根据题意，做出内圈滚动面积A和外圈滚动面积2A。有，

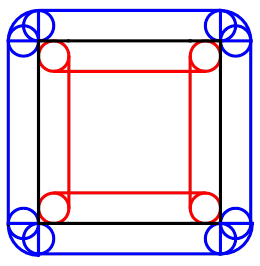
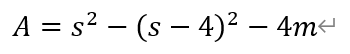
其中，图形m的面积如下图所示，等于四分之一的边长为2的正方形，减去四分之一半径为1的圆，即

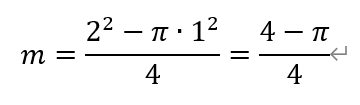
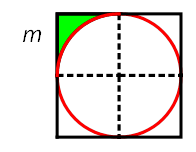
于是，

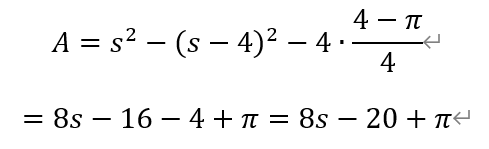
又，2A的面积为，

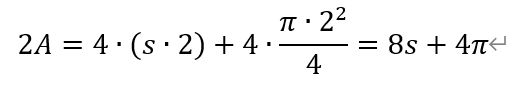
从而有，

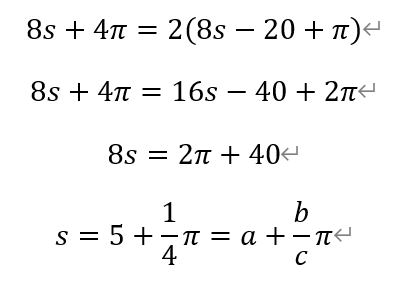
解得，a=5，b=1，c=4。

因此，a+b+c=5+1+4=10。故选A。

[Q20]For how many ordered pairs (b, c) of positiveintegers does neither x²+bx+c=0 nor x²+cx+b=0 have twodistinct real solutions?

A)4    B)6    C)8    D)12    E)16

[答案]B

[解析]若方程x²+bx+c=0没有两个不同的实数根，则有

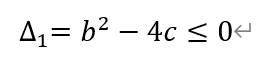
同理，若方程x²+cx+b=0也没有两个不同的实数根，则有

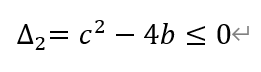
其中，b和c均为正整数。

将这两个方程相加，并整理得，

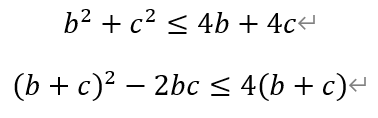
令m=b+c，n=bc，其中m＞0，n＞0，则有

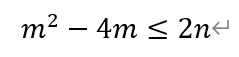
考虑函数f(m)和g(n)，

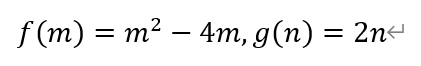
则有，

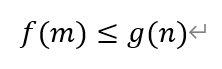
在同一个平面直角坐标系下，分别做出函数f(m)和g(n)的图像，如图所示。

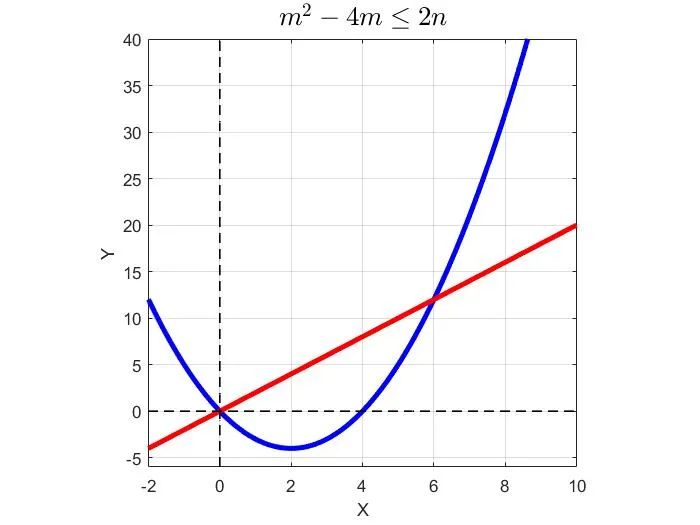
可以看出，当m=8时，f(8)=8×4=32。由于b和c都是正整数，所以在进行正整数拆分时，根据“和同近积大原则”，当b=c=4时，bc的乘积，即n最大。而这个值恰好为g(n)=32。因此m的最大值为8。

由于b和c均为正整数，且还要满足b²-4c≤0，以及c²-4c≤0，所以满足条件的b-c对如下表所示。

综上，符合条件的b-c对为：(1,1)、(1,2)、(2,1)、(2,2)、(3,3)和(4,4)，共6对。故选B。

微信公众号搜索： 北京小学学习资料     家长升学指南  关注公众号，获取最新资讯！

扫码添加“家长论坛”微信好友（微信号 16619908263）

获取迎春杯、数学花园探秘真题、北青研学营、华杯杯赛、华数之星、走美杯、希望杯、美国杯赛大联盟真题
咨询迎春杯、数学花园探秘真题、北青研学营、华杯杯赛、华数之星、走美杯、希望杯、美国杯赛大联盟政策请拨打电话 16619908263 （同微信号）