点击领取>>>北京高考一模、二模、高考试卷真题答案及解析、视频解析

[题目](2021年，北京高考，17)已知正方体ABCD-A₁B₁C₁D₁，点E为A₁D₁中点，直线B₁C₁交平面CDE于点F。

（1）证明：点F为B₁C₁的中点；

（2）若点M为棱A₁B₁上一点，且二面角M-CF-E的余弦值为√5/3，求A₁M/A₁B₁的值．

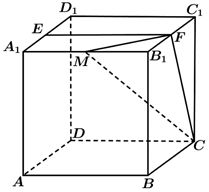
[解析]1）如图所示。

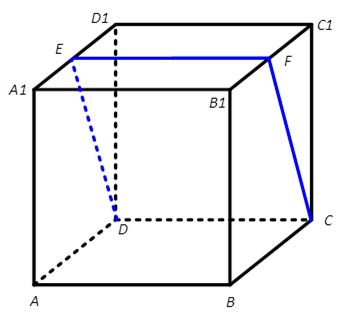
∵正方体ABCD-A₁B₁C₁D₁，∴CD∥C₁D₁。CD不属于面A₁B₁C₁D₁，C₁D₁属于面A₁B₁C₁D₁，∴CD∥面A₁B₁C₁D₁。

又∵CD属于面CDEF，面A₁B₁C₁D₁∩面CDEF=EF，∴根据线面平行的性质定理，CD∥EF。

同时，∵正方体ABCD-A₁B₁C₁D₁，∴面ADD₁A₁∥面BCC₁B₁。面CDEF∩面ADD₁A₁=DE，面CDEF∩面BCC₁B₁=CF，∴根据面面平行的性质定理，DE∥CF。

因此，四边形CDEF的两组对边分别平行，它是一个平行四边形。∴EF=CD。

而CD=C₁D₁，于是在面A₁B₁C₁D₁中，EF=C₁D₁。根据平行线等分线段可知，E为中点，则F也为中点。

2）如图所示，以点D为坐标原点，DA,DC,DD₁分别为x轴，y轴，z轴正方向，建立空间直角坐标系D-xyz。

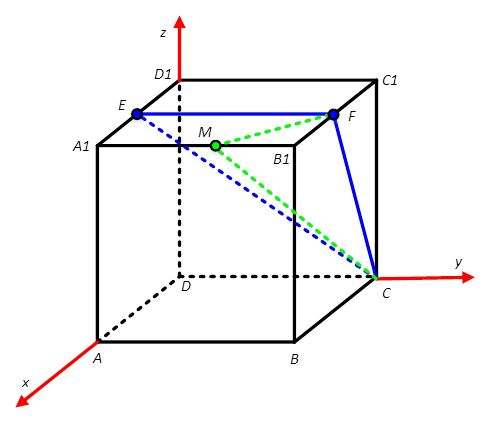
设正方体的棱长为2a，其中a＞0。则各点坐标如下：D(0,0,0)，A(2a,0,0)，C(0,2a,0)，B(2a,2a,0)，D₁(0,0,2a)，A₁(2a,0,2a)，C₁(0,2a,2a)，B₁(2a,2a,2a)，E(a,0,2a)，F(a,2a,2a)。

设A₁M/A₁B₁=λ，λ∈(0,1]。由于A₁B₁=(0,2a,0)，则

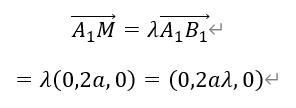
于是点M的坐标为，

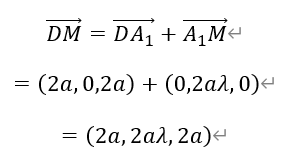
设面MFC的法向量m=(x,y,z)，由于FC=(-a,0,-2a)，FM=(a,2a(λ-1),0)，所以

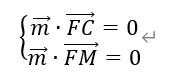
即

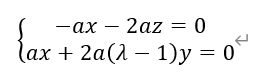
解得，

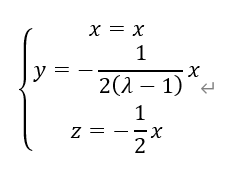
取x=2(λ-1)，则m的一个法向量为：(2(λ-1),-1,1-λ)。

设面EFC的法向量n=(u,v,w)，由于FC=(-a,0,-2a)，EF=(0,2a,0)，所以

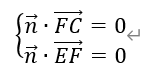
即

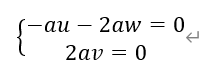
解得，

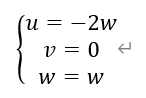
取w=-1，则n的一个法向量为：(2,0,-1)。

从而有

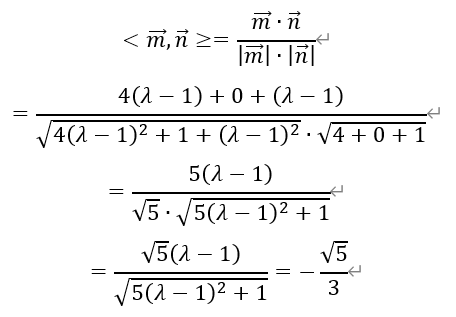
整理得，

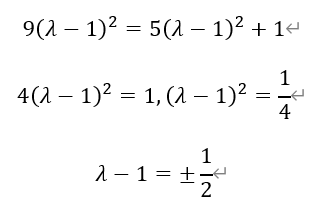
于是，λ=1/2或者3/2。

由于λ∈(0,1]，所以λ=3/2不符合题意，舍去。

故A₁M/A₁B₁的值为1/2。

[后记]客观的讲，2021年北京高考的数学试卷中，基础解答题相对较“坑”，尤其是这道立体几何题。

首先，该题目的第一问，期末、一模和二模的题目都是相对简单的证明，而这里需要综合运用线面平行的性质定理、面面平行的性质定理予以证明。类似的题目在2018年西城期末，以及2020年海淀二模中曾经出现过，全老师在复习时重点进行了讲解。

其次，该题目的第二问，之前普遍预测2021年的立体几何解答题不会考察“存在性问题”。这是根据一模和二模试卷做出的分析，然而期末试卷中部分区县考察了这部分内容。由于考前存在乐观情绪，不少同学认为该部分内容在真题中不会考察，所以本题成了事实上的“中等生杀手”。

需要指出的是，对于优秀学员而言，“存在性问题”依然会重点关注，因为当时的预测是选填的压轴题可能会出立体几何的题目，即立体几何板块会考察“一大两小”题型：其中一“小”指三视图，另外一“小”指选填压轴题。

最后，本题目在计算上相当具有难度。以往在文理分科的年代，理科卷考察“存在性问题”时，若需要算二面角的法向量，则要么第二小问求一个面的二面角，第三小问再求另外一个面的法向量，要么其中有一个面的法向量不需要计算，根据第一小问或者题设直接可以读出，即通常都与某一坐标面平行。然而本题的两个法向量都需要求取，而且参量λ在分母上，不易处理。

微信公众号搜索： 北京小学学习资料     家长升学指南  关注公众号，获取最新资讯！    

扫码添加“家长论坛”微信好友（微信号 16619908263）

获取最新北京高考一模、二模、高考试卷真题答案及解析、视频解析！

咨询北京高中期中、期末、高考相关政策请拨打电话 16619908263 （同微信号）