第四届华杯赛决赛试题及答案

点击领取>>>华杯杯赛、华数之星、华罗庚金杯小中高组夏令营+冬令营+精英赛真题

第四届华杯赛决赛一试试题

1．在100以内与77互质的所有奇数之和是多少？

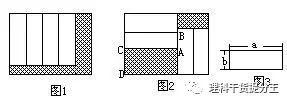
2．图1，图2是两个形状、大小完全相同的大长方形，在每个大长方形内放入四个如图3所示的小长方形，斜线区域是空下来的地方，已知大长方形的长比宽多6cm，问：图1，图2中画斜线的区域的周长哪个大？大多少？

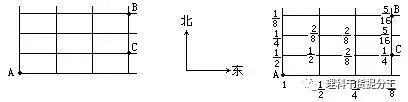
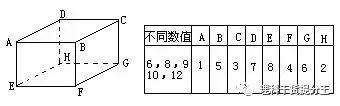
3．这是一个道路图，A处有一大群孩子，这群孩子向东或向北走，在从A开始的每个路口，都有一半人向北走，另一半人向东走，如果先后有60个孩子到路口B，问：先后共有多少个孩子到路口C？

4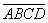．表示一个四位数，
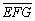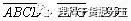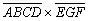表示一个三位数，A，B，C，D，E，F，G代表1至9的不同的数字。已知，问：乘积的最大与最小值差多少？

5．一组互不相同的自然数，其中最小的数是1，最大的数是25，除1之外，这组数中的任一个数或者等于这组数中某一个数的2倍，或者等于这组数中某两个数之和，问：这组数之和最大值是多少？当这组数之和有最小值时，这组数都有哪些数？并说明和是最小值的理由。

6．一条大河有A、B两个港口，水由A流向B，水流速度是4千米/小时。甲、乙两船同时由A向B行驶，各自不停地在A、B之间往返航行，甲在静水中的速度是28千米/小时，乙在静水中速度是20千米/小时，已知两船第二次迎面相遇地点与甲船第二次追上乙船（不算开始时甲、乙在A处的那一次）的地点相距40千米，求A、B两港口的距离。

1.和为1959

2.图1中画斜线区域的周长比图2中画斜线区域的周长大2AB=12cm

3.走过C的人数为48（人）

4.最大值与最小值的差是525000

5.最大值是80，最小值是61，且1+2+3+5+10+15+25=61

6.240千米

1.【解】设A为100以内所有奇数之和，B为100以内不与77互质的全体奇数之和，X为100以内与77互质的所有奇数之和,则 X＝A－B

显然A＝1＋3＋5＋7＋…＋99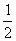＝*50*100＝2500

又77＝7*11

100以内有约数7的奇数之和为7*(1＋3＋5＋7＋9＋11＋13)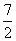＝*7*14＝343

100以内有约数11的奇数之和为 11*(1＋3＋5＋7＋9)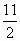＝*5*10＝275

所以B＝343＋275－77＝541

于是，所求之和为 X＝2500－541＝1959．

2.【解】图1中画阴影区域的周长恰好等于大长方形的周长，图2中画阴影区域的周长显然比大长方形的周长小，二者之差是2AB．

从图2的竖直方向看，AB＝a－CD

再从图2的水平方向看，大长方形的长是a＋2b，宽是2b＋CD。己知大长方形的长比宽多6cm．所以

(a＋2b)－(2b＋CD)＝a－CD＝6(cm)，从而AB＝6(cm)

因此，图1中画斜线区域的周长比图2中画斜线区域的周长大 2AB＝12cm。

3.【解】在A处的孩子数目看成1份，那么可顺次标出各道口处走过的孩子的份数，

可见B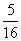处有，C处有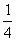。C处孩子总数是 60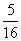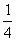＋*＝48(人)

4.【解】

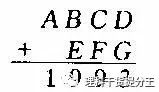
可以看出A＝1，因为E≠0，1，所以B最大为7，这时E＝2由于D、G都不能是O，1，所以D＋G＝13，C＋F＝8由于F≠0，1，2，所以C最大为5。从而三位数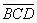最大为759，这时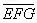＝34。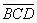最小为234(这时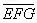＝759最大)。

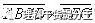＝(1000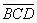＋)*(993－)，

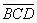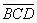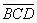＝1000*993－1000*＋993*一*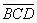

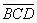
＝993000－7*-－*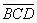

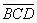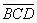
于是在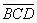最大时，乘积最小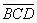，最小时，乘积最大，因此，所求的差是

　(993000－7*234－234*234)－(993000－7*759－759*759)

＝7*(759－234)＋759*759－234*234

＝7*(759－234)＋(759＋234)*(759－234)

＝7*(759－234)＋993*(759－234)

＝1000*（759－234）

＝525000。

5.【解】数组1，2，3，5，10，15，25的和是61，我们证明61就是最小值。

首先25是组中两个数a、b的和，不妨设a＞b，而除去1外，组中最小的数必定是2(否则这最小的数不是两个数的和，也不是1的两倍)。第三个小的数是3或4，在前一种情况，第四个小的数可能是4、5、6；在后一种情况，第四个小的数可能是5、6、8

如果b＞8，那么除去　1，2，3，4…b…a…25(1)

及　1，2，3，5…b…a…25(2)

另外，其它情况各数的和均大于61，而由于b＞8，前一种情况，至少要增加一个大于4的数，各数的和仍大于61，后一种情况，各数的和同样会大于61，除非b＝10，相应地a＝15，即上面所列举的数为61的情况

如果b≤8，那么a≥17，为了将a表示成两个数的和或一个数的两倍，至少要有一个≥9的数，这样各数的和≥1＋2＋3＋b＋9＋a＋25＝65＞61，因此只有数组1，2，3，5，10，15，25使和取得最小值61。

下面，讨论和的最大值，如上所述，除去1外，组中最小的数必定是2，第三个小的数是3或4，在前一种情况，第四个小的数可能是4、5、6；在后一种情况，第四个小的数可能是5、6、8。要使和最大，次大的数可取24，从而数组1，2，4，8，16，24，25的和是80，应为和的最大值。

6.【解】设A、B两个港口相距S千米，甲、乙两船第二次迎面相遇时的位置与港口A相距x千米，甲船第二次追上乙船时的位置与港口A相距y千米。

第一步先求x，甲、乙第二次迎面相遇，甲顺水行(S＋x)千米，逆水行S千米，乙顺水行S千米，逆水行(S－x)千米，甲顺水速度32(＝28＋4)千米／小时，逆水速度24(＝28－4)千米／小时；乙顺水速度24(＝20＋4)千米／小时，逆水速度16(＝20－4)千米／小时，两船所用时间相等，所以

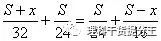
32。24 24。16

即　S十x＝2(S－x)

解得x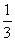＝S

第二步求y．如果甲船在逆水时第二次追上乙，那么乙船顺水行nS千米(n为自然数)，逆水行(nS－y)千米，甲船顺水行(nS＋2S)千米，逆水行(nS＋2S－y)千米，并且

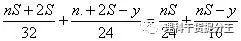
即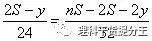　

去分母(两边同乘96)得　(3n－14)S＝2y

由于左边是S的整数倍，右边y＜S，所以必有y＝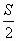

如果甲船在顺水时第二次追上乙，那么乙船顺水行(nS＋y)千米，逆水行nS千米，甲船顺水行(nS＋2S＋y)千米，逆水行(nS＋2S)千米，并且

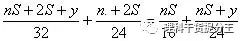
化简得　y＝(14－3n)S(1)

由于14除以3余2，所以(14－3n)≥2S．而

≤

S，从而(1)不能成立

因此，y＝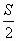

第三步求S

由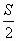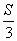－＝40得

S＝40/(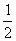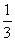－)＝240(千米)

答：两港相距240千米。

第四届华杯赛决赛二试试题

1. 互为反序的两个自然数的积是92565，求这两个互为反序的自然数。(例如102和201；35和53，11和11，…称为互为反序的数，但120和21不是互为反序的数)

2．某工厂的一个生产小组，生产一批零件，当每个工人在自己原岗位工作时，9小时可完成这项生产任务。如果交换工作A和B的工作岗位，其它工人生产效率不变时，可提前一小时完成这项生产任务；如果交换工人C和D的工作岗位，其他工人生产效率不变时，也可以提前一小时完成这项生产任务。问：如果同时交换A与B，C与D的工作岗位，其他工人生产效率不变，可以提前几分钟完成这项生产任务？

3．某校学生中，没有一个学生读过学校图书馆的所有图书，又知道图书馆内任何两本书至少被一个同学都读过，问：能不能找到两个学生甲、乙和三本书A、B、C，甲读过A、B，没读过C，乙读过B、C，没读过A？说明判断过程。

4．有6个棱长分别是3cm，4cm，5cm， 的相同的长方体，把它们的某些面染上红色，使得有的长方体只有一个面是红色的，有的长方体恰有两个面是红色的，有的长方体恰有三个面是红色的，有的长方体 恰有四个面是红色的，有的长方体恰有五个面是红色的，还有一个长方体六个面都是红色的，染色后把所有的长方体分割成棱长为1cm的小正方体，分割完毕后，恰有一面是红色的小正方体最多有几个？

5．小华玩某种游戏，每局可随意玩若干次，每次得分是8，a（自然数），0这三个数中的一个，每局各次得分的总和叫做这一局的总积分，小华曾得到过这样的总积分：103，104，105，106，107，108，109，110，又知道他不可能得到“83分”这个总积分。问：a是多少？

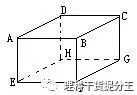
6．在正方体的8个顶点处分别标上1，2，3，4，5，6，7，8，然后再把每条棱两端所标的两个数之和写在这条棱的中点，问各棱中点所写的数是否可能恰有五种不同数值？各棱中点所写的数是否可能恰有四种不同数值？如果可能，对照图a在图b的表中填上正确的数字；如果不可能，说明理由。

1.这两个数是165和561

2.可提前108分钟

3.可以找到满足要求的两个学生

4.最多可得到177个一面为红色的小立方体

5.A=13

6.各棱中点处所写的数恰有五种不同数值是可能的，填法不惟一，但不可能少于五种不同数值

1.【解】

92565＝3×3×5×11×11×17.

互为反序的两个自然数中，若其中之一为3的倍数(或11的倍数)，另一个也必为3的倍数(或11的倍数).又因乘积是五位数，所以这两个数是三位数，我们有

92565＝(3×5×11)×(3×17×11)＝165×561

　于是,这两个数为165和561

2.【解】把总任务分成72份，原来每小时完成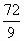＝8份，每份要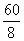＝7.5分钟

　A与B交换后，每小时完成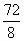＝9份，比原来多干了1份，由于其他人工效不变，

　所以这一份就是A、B二人多干的。

同理，C与D交换后，他们二人每小时也要多干1份任务。同时更换后,A与B、C与D每小时都多干一份任务，所以全组工人每小时干了8＋1＋1＝10(份)任务，即每份任务只要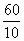＝6(分钟)就能干完。因此每干1份任务，提前7.5－6＝1.5(分钟)。72份任务一共提前请点击此处输入图片描述

72×1.5

＝108(分钟)。

3.【解】首先从读书数最多的学生中找一人甲，由题设，甲至少有一本书C未读过。

设B是甲读过的书中的一本，根据题设，可找到学生乙，乙读过B、C。

由于甲是读书数最多的学生之一，乙读书数不能超过甲的读书数，而乙读过C书，甲未读过C书，所以甲一定读过一本书A，乙没读过A书，否则乙就比甲至少多读过一本书，这样一来，甲读过A、B，未读过C；乙读过B、C耒读过A。因此可以找到满足要求的两个学生。

4.【解】一面染红的长方体，显然应将4*5的长方形染红，这时产生20个一面红的小正方体，个数最多

二面染红的长方体，显然应将两个4*5的长方形染红，这时产生40个一面红的小正方体，个数最多三面染红的长方体，应将4*5，4*5，4*3的面染红，产生4*(5＋5＋3－4)＝36个一面红的小正方体，其它方法得出的一面红的正方体均少于36个。四面染红的长方体，应将4*5，4*5，4*3，4*3的面染红，产生4*(5＋5＋3＋3－2*4)＝32个一面红的小正方体，其它方法得到的一面红的小正方体均没有这么多五面染缸的长方体，应只留一个3×5的面不染，这时产生(3－2)(5－2)＋(4－1)(5＋5＋3＋3－2*4)＝27个一面红的小正方体，其它染法得到的一面红的小正方体均少于27六面染红的长方体，产生 2[(3－2)(5－2)＋(5－2)(4－2)＋(4－2)(3－2)]＝22 个一面红的小正方体。于是最多得到 22＋27＋32＋36＋40＋20＝177 个一面红的小正方体

5.【解】83＋8*3＝107，所以在得到总积分107时，得8分的局数必定小于3(否则83＝107－3*8可以得到)，即得8分的局数为0、1或2，从而107，107－1*8＝99，107－2*8＝91这三个数中必有一个是a的倍数。

如果107是a的倍数，那么a＝1或107，但a＝1时，可以得到总积分83；a＝107时，无法得到总积分103，所以这种情况不可能发生。

如果99是a的倍数，那么a＝1，3，9，11，33，99。

因为83＝9*3＋8*7＝11＋8*9，所以a不能是1，3，9，11(否则83可以得到)。

因为103＝99＋14＝33＋70＝2*33＋37，所以a＝99或33时，无法得到总分103。

因此这种情况也不可能发生。

如果91是a的倍数，那么a＝1，7，13，91，因为83＝7*5＋8*6，所以a

≠

7.1 103＝91＋12，所以a

≠

91。

因此a＝13，不难验证a＝13符合要求。

6.【解】各棱中点处所写的数恰有五种不同数值是可能的，如在A、B、…、H依次填1,5、3、7、8、4、6、2，则中点处恰有五个不同数值6、8、9、10、12。

不可能少于五种不同数值，理由如下：

以1所在顶点为端点的棱有三条，不妨设这三条棱的另一端点所填写的数是a、b、c，满足a＜b＜c，则这三条棱的中点处的数为1＋a，1＋b和1＋c，满足1＋a＜1＋b＜1＋c。

以8所在顶点为端点的棱也有三条，不妨设这三条棱另一端点所填写的数为x、y、2，满足x＜y＜z，则这三条棱的中点处的数为8＋x，8＋y，8＋z，满足8＋x＜8＋y＜8＋z。

又 c≤8，1＋c≤9；x≥1，8＋x≥9，

所以 1＋a<1＋b<1＋c≤8＋x＜8＋y＜8＋z

从而这六条棱中点的六个数不可能少于五种不同的值，因此在12条棱中的点处所写的数不可能有少于五种不同的数值。

微信公众号搜索： 北京小学学习资料     家长升学指南   家长升学训练营  关注公众号，获取最新资讯！  

扫码添加“家长论坛”微信好友（微信号 16619908263）

获取华杯杯赛、华数之星、华罗庚金杯小中高组夏令营+冬令营+精英赛真题

咨询华杯杯赛、华数之星、华罗庚金杯政策请拨打电话 16619908263 （同微信号）