2021 美国"大联盟"(Math League)国际夏季数学挑战活动

点击链接>>>美国数学大联盟杯赛真题、数学常用词汇表

夏季速度赛，45分钟完成60题，快速理解题意非常重要，学习找关键词，部分翻译并适当猜测考察什么知识，有助于我们更快更准答题。下面以2021美大夏赛五年级速度赛试卷为例，尝试抓取类似下文黄色部分信息来快速理解大致题意。

2021 美国"大联盟"(Math League)国际夏季数学挑战活动

2021 Math League International Summer Challenge

Grade 5, Speed Questions

1. (2021 ÷5) + (2021 ÷5) + (2021 ÷5) + (2021 ÷5) + (2021 ÷5)    =

A) 2020                 B) 2021               C) 2022               D) 8084

2. Kirok the dragon has 2021 scales on his neck, 3031 scales on his wings, and 5051 scales on the rest of his body. What is the total number of scales on Kirok’s body?

A) 1013                 B) 7073               C) 10103             D) 100103

3. What is the remainder when (7 + 77 + 777 + 7777 ) is divided by 7?

A) 0                       B) 1                     C) 4                     D) 1234

4. Four out of every five dentists recommend HiGlo toothpaste. If I ask 100 dentists whether they would recommend HiGlo toothpaste, how many of the dentists will     recommend it?

A) 25                     B) 30                   C) 50                   D) 80

5. What is the perimeter of a square that has an area of 64?

A) 16                     B) 24                   C) 32                   D) 64

6. 4 × 5 × 101 = 1010 ×  ? 

A) 2                       B) 20                   C) 101                 D) 1010

7. Each angle of a rectangle is  ? degrees greater than each angle of an equilateral triangle.

A) 30°        B) 60°       C) 90°       D) 120°

8. It is 2021 hours after midnight. What time is it?

A) 5 AM                B) 7 AM              C) 5 PM              D) 7 PM

9. If 20% of a number is 50, what is 40% of the same number?

A) 30                     B) 60                   C) 100                 D) 150

10. As he rides, Sir Reginald von Prime is going to plant a flag every time the total  distance he has ridden is a prime number of km. How far will he have gone when he plants his 11th flag?

A) 23 km               B) 29 km             C) 31 km             D) 37 km

11. The greatest common factor of 43  × 52 and 53  × 72 is

A) 5                       B) 52                              C) 53                              D) 55

12. How many 2-digit odd numbers do not have 3 as either digit?

A) 32                     B) 36                   C) 40                   D) 44

13. My average score on the 3 tests I’ve taken so far is 85. What score do I have to get on the next to raise my average score to 88?

A) 94                     B) 95                   C) 96                   D) 97

14. 

Nan knits new tops for newborns.Today she knitted one more top than yesterday. The number of tops she knitted in the two days combined could be

A) 12                     B) 23                   C) 34                   D) 100

15. 8 dozen socks =   ?   pairs of socks

A) 24                     B) 36                   C) 48                   D) 96

16. A boy is in line with 30 people behind him and twice as many ahead of him. How many people are in this line?

A) 60                     B) 61                   C) 90                   D) 91

17. If the sum of 6 consecutive integers is 255, what is the sum of the greatest and the least of the integers?

A) 38                     B) 43                   C) 81                   D) 85

18. Paola ran the 300 m from her door to the bus in 20 seconds. What was her speed in km/hr?

A) 15                     B) 20                   C) 34                   D) 54

19. What is the product of all the positive divisors of 64?

A) 64                     B) 8 × 642                 C) 8 × 643                 D) 644

20. In 30 years my age will double, my sister’s age will triple, and my brother’s age will quadruple! What is the sum of our ages now?

A) 32.5                  B) 55                   C) 90                   D) 100.5

21. The greatest prime factor of the number of seconds in 2197 hours is

A) 11                     B) 13                   C) 17                   D) 19

22. In the country of Latka, 6 simkas are worth 25 ibidas and 2 ibidas are worth 15 yatabes,If I pay 12 simkas for a chicken that is priced at 365 yatabes, how many   yatabes should I expect in change?

A) 10                     B) 12                   C) 13                   D) 15

23. A lighthouse can be seen from at most 50 km on a clear night but from at most 20 km during fog. The greatest viewing distance on a clear night is what percent of the   greatest during fog?

A) 40                     B) 60                   C) 150                 D) 250

24. What is the greatest possible number of points of intersections of a circle and a rectangle?

A) 2

B) 4

C) 6

D) 8

25. How many squares of integers have 3 digits?

A) 20                     B) 21                   C) 22                   D) 23

26. Al writes the first 20% of his report on Monday, then 30% of the remaining report on Tuesday. What percent of the entire report that Al began on Monday remains to be written on Wednesday?

A) 44%                  B) 50%                C) 54%                D) 56%

27. 42 ×44  ×46  ×48 =

A) 240                               B) 41024                        C) 1630                         D) 6430

28. Zak shuffled together four decks of cards and started dealing them out. Surprisingly, the suits came out in a pattern that repeated as follows until the 26th club appeared: club, diamond, heart, club, heart, diamond, club, diamond, heart, club, heart, diamond, ....     How many cards must Zak deal in order to have dealt 26 of the club suit?

A) 75                     B) 76                   C) 78                   D) 84

29. My

local ice cream shop offers 15 different flavors of ice cream.If I want two scoops of ice cream, each scoop a different flavor, how many combinations of two scoops of ice      cream are possible?

A) 29                     B) 30                   C) 105                 D) 210

30. Inez multiplied 21 by the product of 21 21s. Then she subtracted 21 from that product 2121 times. With what number did she end up?

A) 0                       B) 2120                         C) 2121 + 212          D) 2122 – 212

31. What is the greatest number of prime factors (not necessarily all different) that a three-digit number can have?

A) 5

B) 6

C) 8

D) 9

32. How many of the first 2021 even positive integers are divisible by 6?

A) 336                   B) 337                 C) 673                 D) 674

33. Maestro must be able to divide the birds in his all-bird choir into 6, 7, and 8 equal groups. He wants a 3-digit total number of birds. In all, how many such 3-digit numbers are possible?

A) 2                       B) 3                     C) 4                     D) 5

34. If 25 people take 27 hours to catch all the birds, at that rate how long would it take

45 people to catch all the birds?

A) 9 hrs                 B) 15 hrs             C) 18 hrs             D) 21 hrs

35. What is theleast number of consecutive positive integersstarting with 1 that must be multiplied together to get a multiple of 2021?

A) 22                     B) 80                   C) 90                   D) 105

36. (2 + 4 + 8)2 =

A) (3 + 4 + 5)2

B) (4 + 5 + 6) ×2

C) (1 + 2 + 4)2 ×4

D) 22 + 42 + 82

37. Each equilateral triangle shown has a perimeter of 9. What is the perimeter of the figure?

A) 6                       B) 8                     C) 10                   D) 12

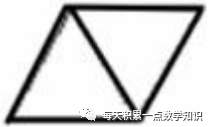
38. The base of an isosceles triangle with integral sides is 12. What could be the perimeter?

A) 20                     B) 22                   C) 24                   D) 26

39. Emma counted up from 0 by 1s every second for 5 minutes, and then down by 1s every second for 2 minutes. What number did she end on?

A) 180                   B) 240                 C) 360                 D) 480

40. What is the 200th number in the sequence 1, 1, 1, 2, 1, 3, 1, 4, 1, 5, ...?

A) 1                       B) 100                 C) 101                 D) 200

41. 2020is divisible by  ?  different prime numbers.

A) 2                       B) 3                     C) 4                     D) 5

42. The larger angle between the minute hand and the hour hand of a circular clock at 1:10 PM measures

A) 300°       B) 315°      C) 330°      D) 335°

43. How many prime numbers less than 50 have reciprocals that are terminating decimals?

A) 1

B) 2

C) 3

D) 4

44. Red pens are sold at 3 for $1 and black pens are sold at 4 for $1.50. Alice bought

12 red pens and 24 black pens. She paid for them with a $20 bill.How much change did she receive?

A) $7                     B) $9                   C) $13                 D) $16

45. The number 1000 has only 16 positive whole number factors. The product of all

16 of these factors is

A) 108                              B) 1016                         C) 1024                         D) 1032

46. The average of 21 consecutive integers is 31. The largest of these integers must be

A) 40                     B) 41                   C) 51                   D) 52

47. (221 × 1000) + (221 × 100) + (221 × 10) + (221 × 1) is divisible by

A) 2                       B) 3                     C) 4                     D) 11

48. 314159272 – 314159262 = 31415926 +  ?

A) 0                       B) 31415927       C) 31415928       D) 31415925

49. Each km of a 5 km race, my horse’s average speed decreased 1 km/hr. If I averaged

5 km/hr at first, it took me  ?  minutes to finish.

A) 120                   B) 137                 C) 216                 D) 685

50. I make a straight cut through a rectangular piece of paper and get two pieces. When I make a straight cut through one of these two pieces, I then have three pieces.             Altogether, the number of edges on these three pieces cannot be

A) 8                       B) 9                     C) 10                   D) 11

51.

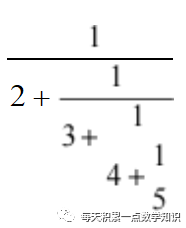is equivalent to

A)  

B)  

C)  

D) none of these

52.

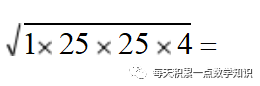
A) 4                       B) 25                   C) 50                   D) 100

53. If the total value of an equal number of pennies, nickels, and dimes is $3.20, what is the value of the nickels alone?

A) 40 cents            B) 60 cents          C) 80 cents          D) 100 cents

54. What is the ones digit of 22021?

A) 2                       B) 4                     C) 6                     D) 8

55. The sum of 50 consecutive whole numbers equals the sum of 25 other consecutive whole numbers. If the smallest of the 50 numbers is 2021, the smallest of the 25          numbers is

A) 4079                 B) 4103               C) 2021               D) 2070

56. If B is the midpoint of AC , and if C is the midpoint of BD , then what percent of CD is AC?

A) 25%                  B) 50%                C) 100%              D) 200%

(  1  100

57. If 

, then the total number of times that a 0appears to the right of the decimal point and left of the 1is

A) 98                     B) 99                   C) 100                 D) 101

58. I plan to give a total of 3 (identical) slices of pizza to Ali, Bob, and Carl. Each      person will get 0, 1, 2, or 3 slices. In how many different ways can I distribute these 3 slices of pizza?

A) 8                       B) 9                     C) 10                   D) 12

59. All the whole numbers with a first digit of 2 are written in increasing order. The list begins 2, 20, 21, 22, .... Find the 1000th digit thus written.

A) 6

B) 7

C) 8

D) 9

60. A perfect square is the square of an integer. Of the integers from 2 through 99 inclusive, how many have at least one perfect square factor > 1 ?

A) 36                     B) 38                   C) 40                   D) 44

微信公众号搜索： 北京小学学习资料     家长升学指南  关注公众号，获取最新资讯！ 

扫码添加“家长论坛”微信好友（微信号 16619908263）

获取美国数学大联盟杯赛真题、数学常用词汇表
咨询美国数学大联盟杯赛政策请拨打电话 16619908263 （同微信号）