2023深圳中考数学全卷完整版和压轴题解析
点击领取>>>深圳中考真题、深圳各区一模、二模、三模试卷真题及答案解析汇总


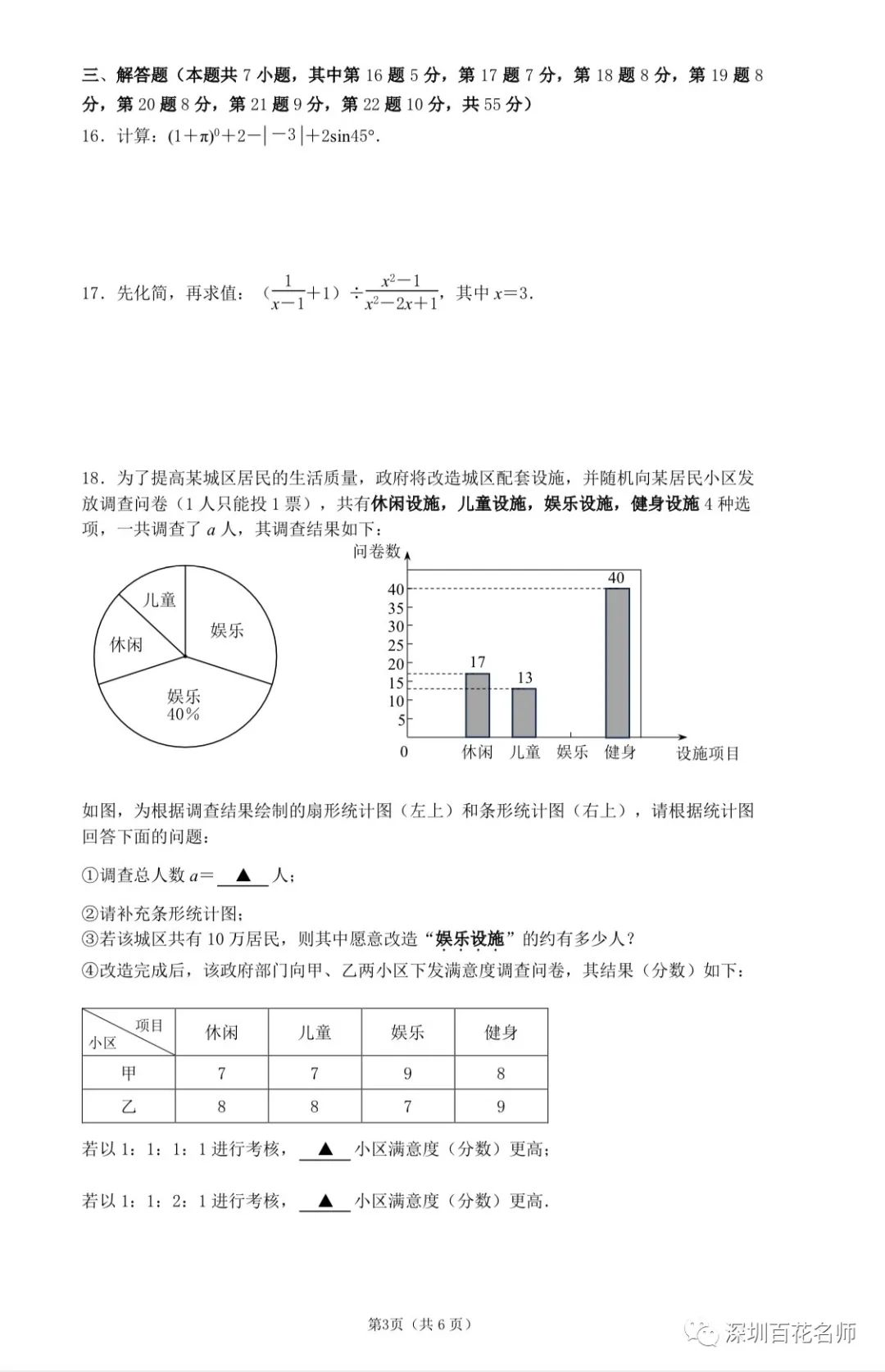
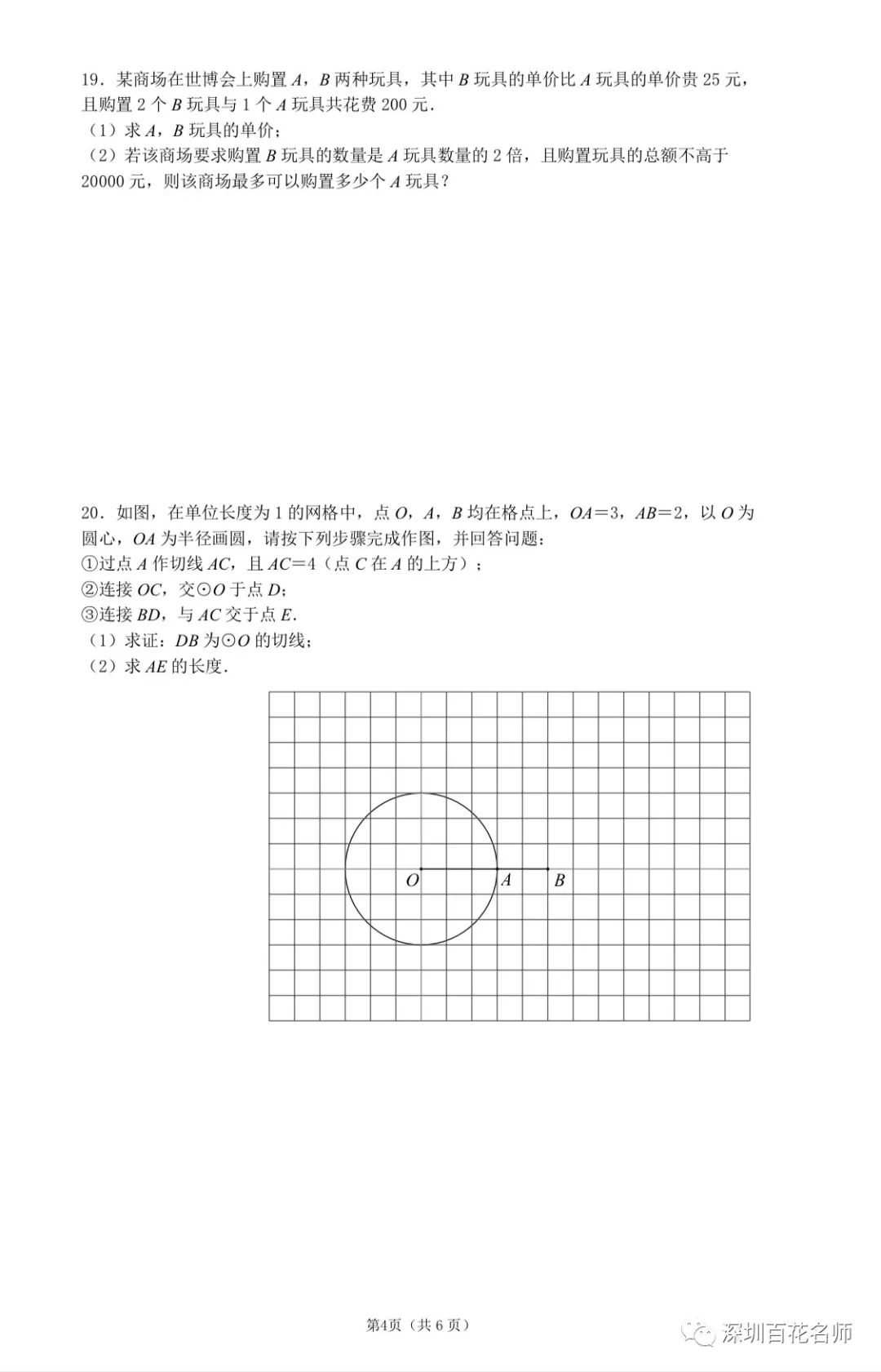

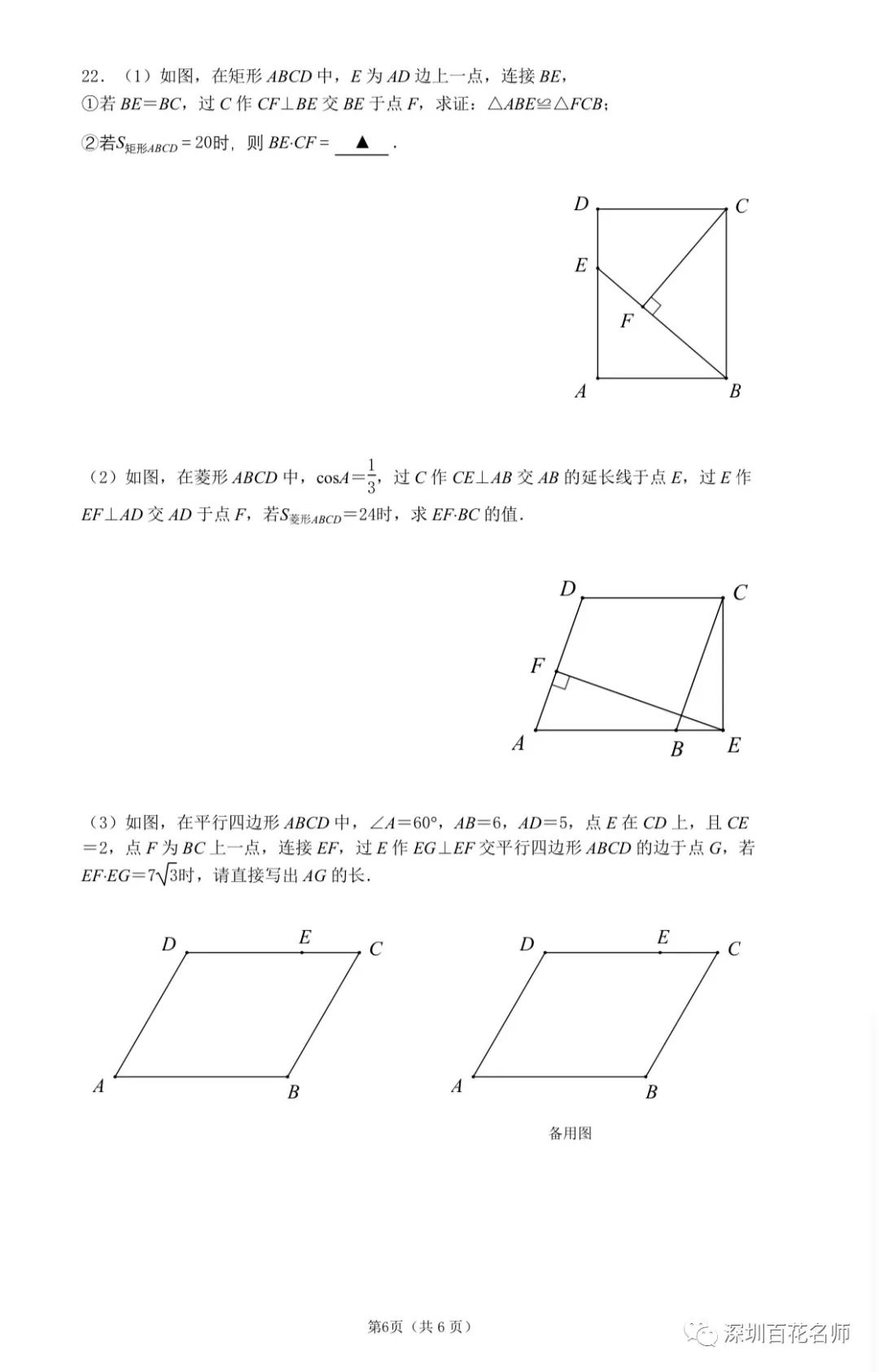
1) 略有创新,趋势不变
试卷中最大的创新就在选择题第10题和第21题,几何作为压轴的趋势并未变化,15题依旧是相似,22题依旧是几何探究。第10题的动点函数问题有所创新,但属于常规题;第21题的二次函数实际应用题,在2021年第20题就有所涉及
创新题-21题一览(更正:以下右侧均为2023年中考题)
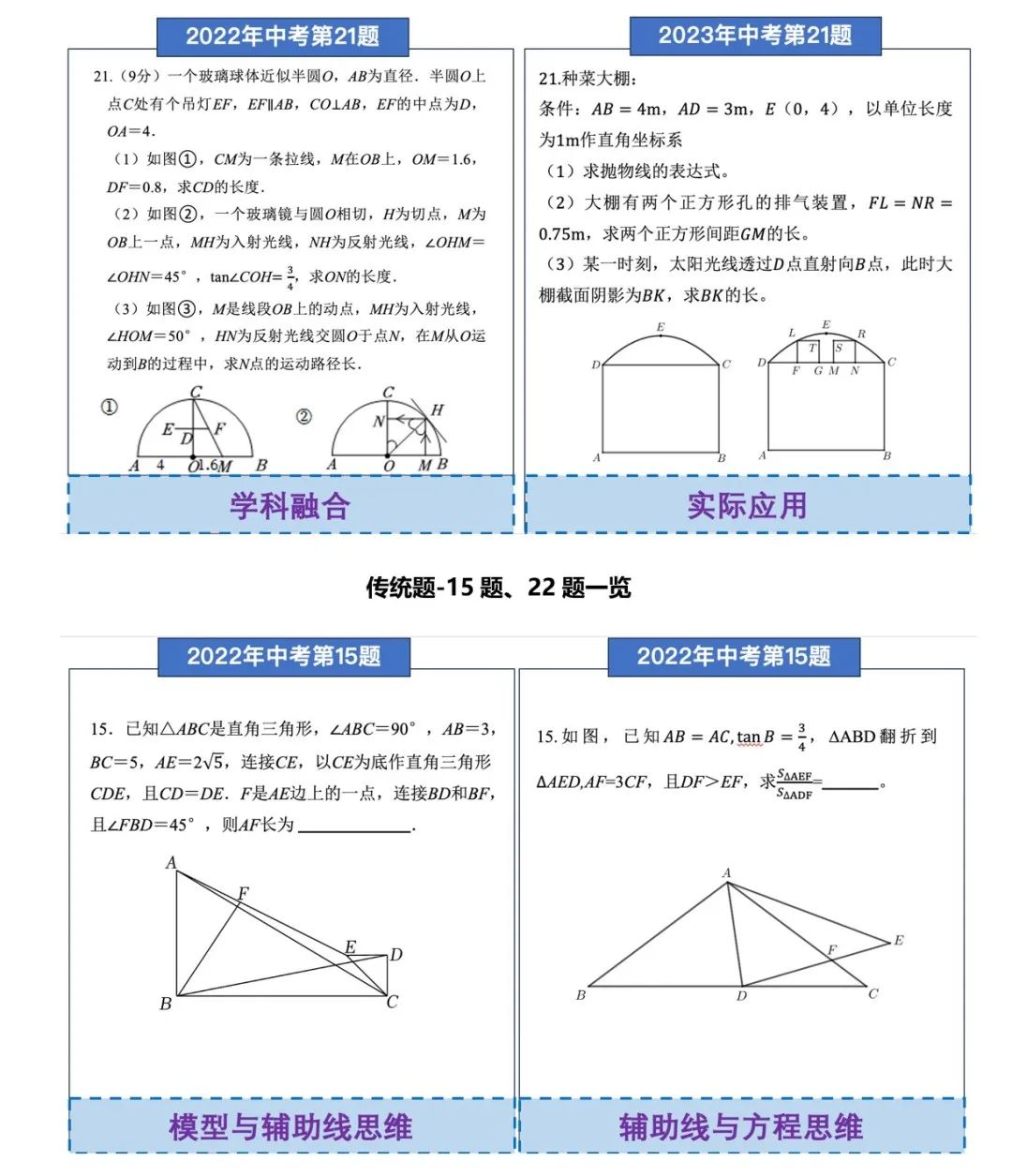
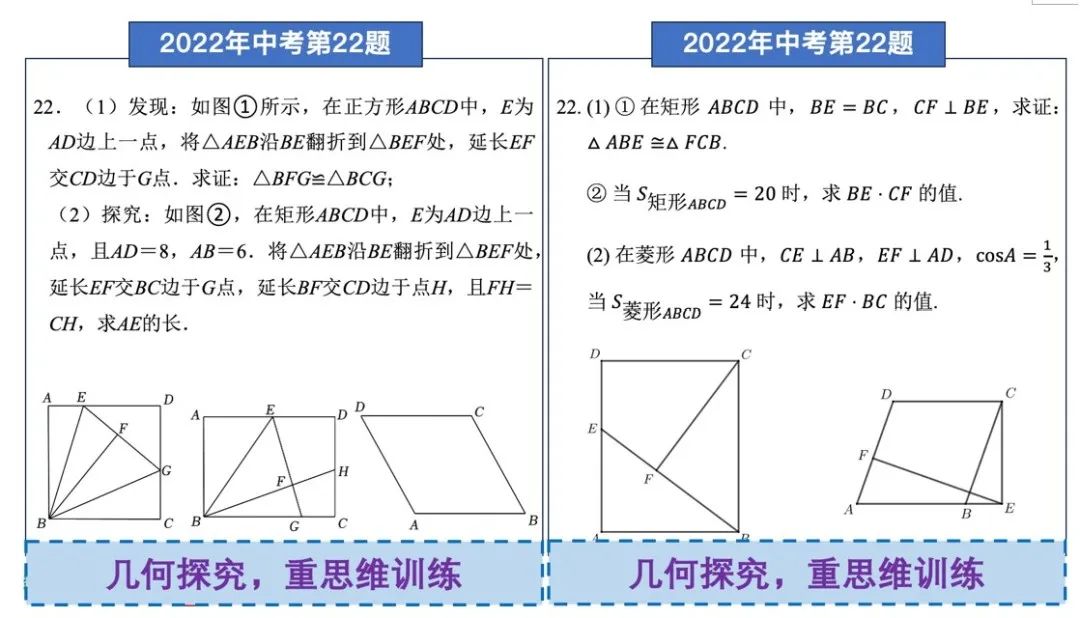
△点击图片可放大查看
2) 难度降低,重在基础
试卷整体难度有所降低,选择1-10题、填空11-14题、解答题16-20以及21(1)、22(2)都没什么难度,整体分值去到88分,所以基础不错的孩子都可以达到一个不错的分数,预计今年的数学A+线会略有上浮。
3) 压轴考点,模考涉及
本次考试最难的题目为15题和22题,15题弱化了模型的考查,重点在于利用辅助线构造相似,获得线段之间的关系,建立方程求解是关键,是几何和代数的结合,22题还是四边形和模型相结合。
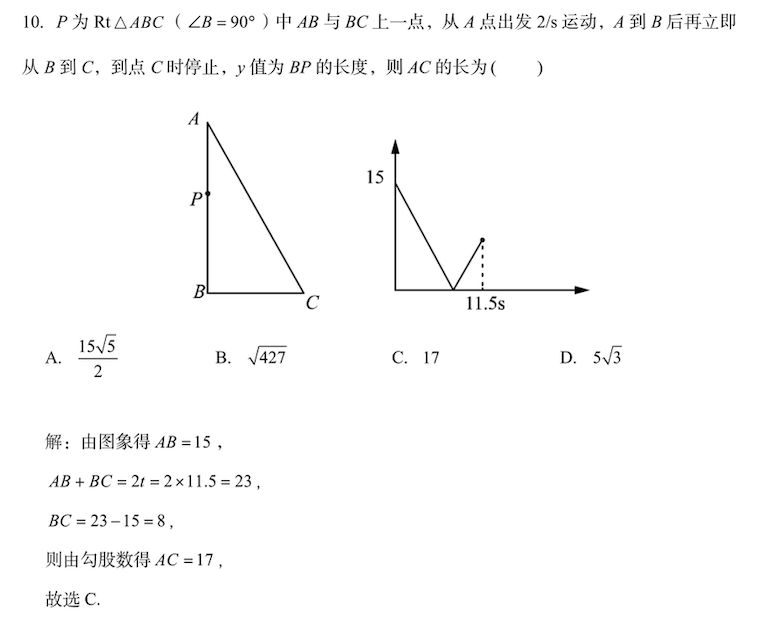
第10题(选择压轴题)
第15题(填空压轴题)
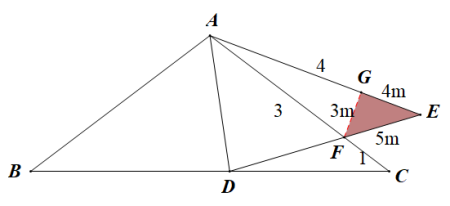
15.如图,已知AB=AC,tan∠B= ,将△ABD沿AD折叠,且满足AF=3FC(DF>EF),此时
,将△ABD沿AD折叠,且满足AF=3FC(DF>EF),此时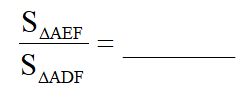
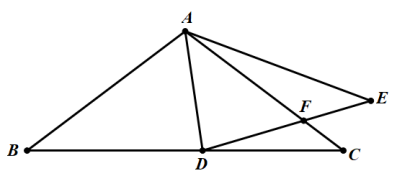
解:方法一:作AG⊥BC、AH⊥DE,易知AG=AH,设AF=3m,则CF=m,AG=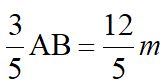 ,EH=BG=
,EH=BG=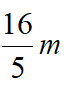 ,故FH=
,故FH=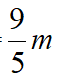 得EF=EH-FH=
得EF=EH-FH=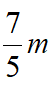 ,而由△AEF~△DCF得
,而由△AEF~△DCF得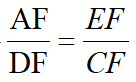 得DF=
得DF=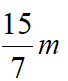 ,得
,得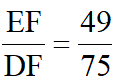 ,故
,故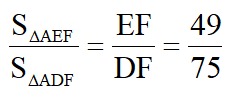
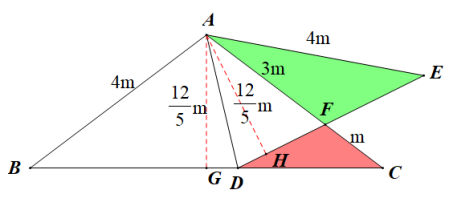
方法二:作FG⊥AE于点G,设CF=1,则AF=3,AC=AE=AB=4,设EF=5m,则FG=3m,GE=4m,在AGF中,有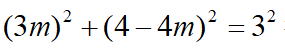 得
得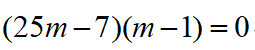 得m=1(舍)或
得m=1(舍)或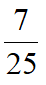 ,得EF=
,得EF=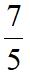 ,而由△AEF~△DCF得
,而由△AEF~△DCF得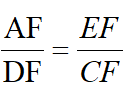 得DF=
得DF= ,得
,得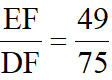 ,故
,故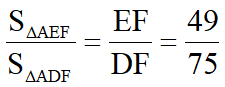
第22题(解答压轴题)
22.(1)在矩形ABCD,BE=BC,CF⊥BE,求证:△ABE≌△FCB
当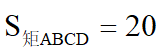 时,求BE·CF=____20_______
时,求BE·CF=____20_______
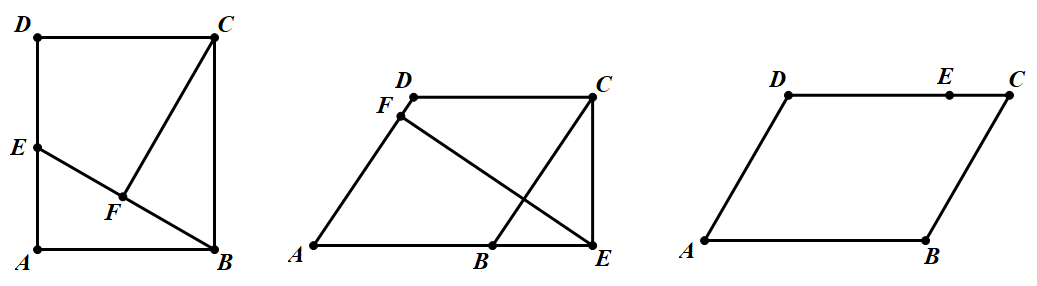
(2)菱形ABCD,CE⊥AB,EF⊥AD,cosA=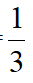 ,当
,当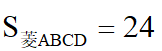 ,求EF·BC=_______
,求EF·BC=_______
(3)平行四边ABCD中,∠A=60°,AB=6,AD=5,CE=2,F为BC上任意一点,作EF⊥EG,交平行四边形ABCD的边于点G,当EF·EG=7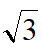 时,直接写出AG的长.
时,直接写出AG的长.
解:(2)易知△AEF~△BCE,得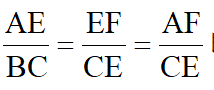 即有AE·CE=EF·BC,而AE=AB+BE=AB+
即有AE·CE=EF·BC,而AE=AB+BE=AB+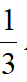 AB=
AB=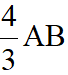 ,即EF·BC=
,即EF·BC= AB·CE=
AB·CE= ×24=32
×24=32

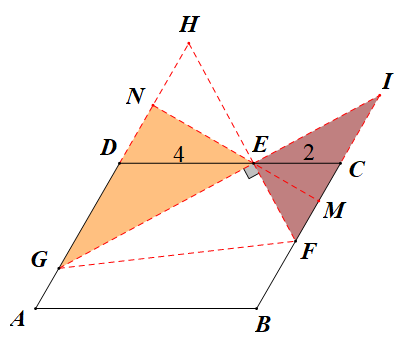
(1) ①当点G在AD上时,如图,延长GE交BC延长线于点I,过E作MN⊥AD于点N,交BC于点M,易知△ENG~△FEI,得EF·EG=EN·FI,而EN=2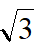 ,得FI=
,得FI=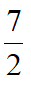 ,设FM=m,则MI=
,设FM=m,则MI=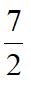 -m,由射影定理得EM2=FM·MI,即有(
-m,由射影定理得EM2=FM·MI,即有(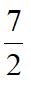 -m)m=3得m=2或
-m)m=3得m=2或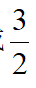 得CI=1或
得CI=1或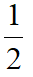 ,由DG=2CI得DG=2或1,于是AG=3或4
,由DG=2CI得DG=2或1,于是AG=3或4
②当G在AB上时,如下左图所示过点G作GQ||AD交FE延长线于点Q,易得△EFP~△GQE得EF·EG=EP·GQ,得GQ=7,得QH=2,作QT⊥AB于点T交CD于点S,作GV⊥CD于点V,设SE=m,由△EQS~△GEV得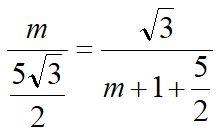 得m=
得m=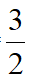 得DH=
得DH=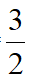 故AG=
故AG=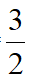 ;(亦可由下右图解决,原理一致)
;(亦可由下右图解决,原理一致)
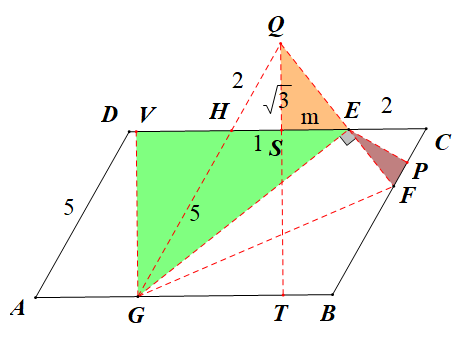
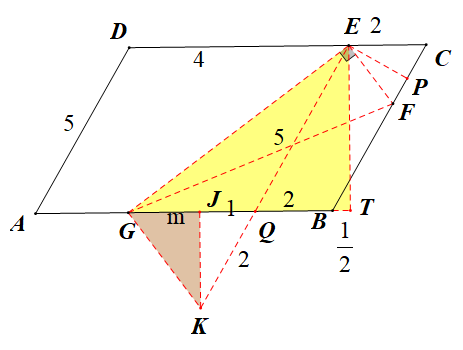
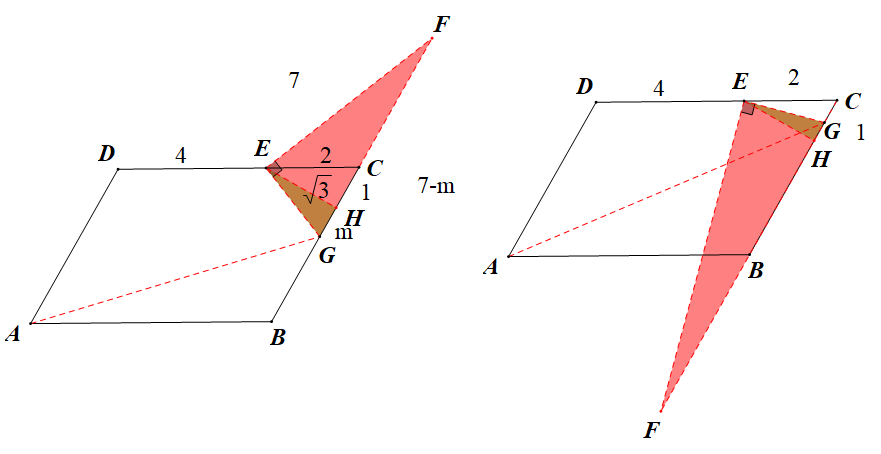
③G在BC上时,此时F在BC的延长线上,如下左右图
左图,易知△EFH~△GFE,得EF·EG=EH·GF,得GF=7,设GH=m得FH=7-m,由射影定理得GH·FH=EH2,即有(7-m)m=3,得m=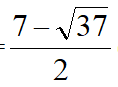 (左图数据)或
(左图数据)或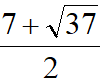 (右图数据),后续数据过于复杂,交给大家讨论
(右图数据),后续数据过于复杂,交给大家讨论
微信公众号搜索: 家长升学训练营 关注公众号,获取最新资讯!

扫码添加“家长论坛”微信好友(微信号 16714210308 )
获取深圳中考真题、深圳各区一模、二模、三模试卷真题及答案解析汇总
咨询深圳初中、中考考试等相关政策请拨打电话 16714210308 (同微信号)
没有找到相关结果
0 个回复