华数之星3.26南京线下活动解析与简评

点击领取>>>华杯杯赛、华数之星、华罗庚金杯小中高组夏令营+冬令营+精英赛真题

整体来看，还是华数之星中规中矩的风格，1,2，3,4，7题，都是非常成熟的陈题，经过系统的奥数学习，思维难度偏低；5,6题结合一些具体情境，相对是有难度的，会是拉开差距的问题，作对6道及以上的孩子，基本功是非常扎实的。作对3道及一下，说明题目练习非常不足，需要特别加强基础中档题目的练习。

第1题

北京冬奥会的开幕式是 2022 年 2 月 4 日，闭幕式是 2022 年 2 月 20 日，残奥会开幕式是2022 年3 月4 日，闭幕式是2022 年3 月13 日，已知2022 年3 月13 日是星期日，问 2022 年2 月4 日是星期__________

答案：五

解析：枚举。日期-7，星期不变。3月6日，2月27日，20日，13日，6日均为星期日，则2月4日为星期五。或者计算：（24+13）÷7....2，星期日往前倒2天，星期五。

评析：2星 周期问题

常规周期问题，但是非常容易出错，一方面是2月是28天，另一方面，倒推时间非常容易出错，如果是正向思考，比如下面这道青岛三年级期末测试题，用的同样的冬奥会背景，解决起来就容易许多。

第2题

把 0 ~ 9 分别填入下面的方框内，每个数字只能用一次，使得算式的结果最小. 那么这

个结果是__________.

答案：1468

解析：位权分析 上述□ ：abcd+ efg+ hi ×j

a:1000      b:100     c:10     d :1     e:100   f:10

g:1    h:10×f       i:f           j:hi

使结果最小，位权大的数放小的数字，a=1,b,e放0和2，由于0不能作首位，所以b=0,

评析：4星  数字谜+最值

如果没有学过位权分析或者由位值的意识，作对非常困难。问题本身属于一个陈题。比如2021年希望数学100题五年级的题目：

都是位权分析，答案分别是

73×（65+4）+1×2=5039

第3题

答案：221

解析：

数字和：1×195+9+8+9=221

评析：3星   大数的计算 乘法分配律巧算

很多三四年级看到省略号就害怕，题目难度其实不大，克服恐惧的心理。刚好这学期开学就讲了类似的问题，第一次测试也考了相关题目，学生下来表示这道题很有把握。

第4题

某医院安排了 5 个注射室接种新冠疫苗，每个注射室每次只能接种一人，如果有两人来到了同一个注射室，就需要排队. 一天有 3 人同时来到医院接种疫苗，如果他们选择哪一个注射室都是随机的，则有多少种可能的排队方式？

答案：210

解析：加乘原理，分类讨论

（1）三人选择同一科室：选科室，5种，3个人排队：3×2×1=6（种）共5×6=30（种）

（2）2人相同，一人不同，3人中先选1人单独去一个科室，3种选法，1人先选1个科室，5种选法；剩余2人选科室，4种选法，然后两人顺序互换2种

3×5×4×2=120（种）

（3）3人不同 第1个选择5种，依次4种和3种，共5×4×3=60（种）

共30+120+60=210（种）

评析：3星  加乘原理

加乘原理是中年级计数最核心的原理，当然高年级也特别重要，先分类再分步，从而得出正确的解。

第5题

有一个 45 环的链条，从中间剪断一些铁环，会得到一些短链条和断环. 把它们分成 9

组，使每一组至少有一个环，且各组环的数量互不相同（断环按 1 个环计算数量），请问最少要剪断几个环？

答案：6

解析：9组铁环每组至少1个，互不相同，只能是1+2+3+4+...+9=45(个）

大数可以剪出来，小数由断环拼凑。先论证最少的情况。

9+8+7+6=30环，此时有4个断环和11个环，11＞9，如果分成2段，则最长最少=6，不符合题意，至少再分2次，共6次

再构造，剪出9,8，7,6，5,4的链条，还剩6个断环，分成3个，2个，1个三堆。

评析：4星  构造论证

在华数之星中年级的构造论证中，难度属于比较低的类型，但是相对于其他题目，我还是比较喜欢这道题的，至少把最值的思想嵌合进一个实际问题中，是这套题里面相对比较有新意的问题，文字结构值得加一星。

第6题

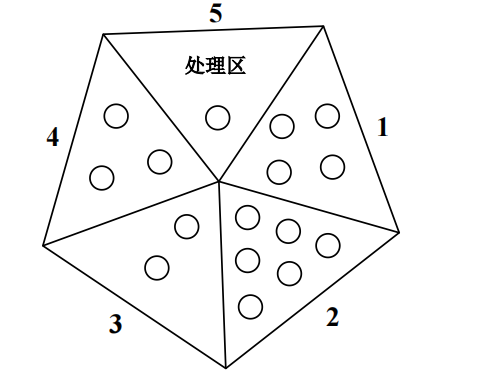
甲、乙两人在玩一款双人游戏，玩家可以在 1 ~ 4 号区域里选择任意数量的棋子（要小于等于区域内原有的棋子数量），顺时针向前移动到下一个区域. 最终谁把最后一个棋子移动到 5 号区域（目标区），谁就获胜. 现在甲遇到如下图的局势，请问他要从

__________区移动__________颗棋子，才能必胜

答案：必胜策略问题

显然题目使用对称法，构造对称，区域5的棋子不用管，同理，区域三也不用管，因为如果你移动区域三a颗棋子到区域四，那么我紧接着就可以移动相同颗数到区域五；类似的，区域一也不用管，可以移动到区域三。

我们观察区域2和4，对称即可。所以把区域二移动3颗到区域四，乙怎么移动，不管乙怎么拿，甲保持区域2和区域4数量相同即可。

评析：4星  必胜策略

必胜策略的两种思路：找逆推法必胜点和对称法，这道题都综合运用到了。所以还是有意思的。北京市的早培2022年入营下午的练习题也都是必胜策略问题。比较有意思，

下面出一道，看有没有哪位同学能够解的：

第7题

将一个八位正整数 n 输入，按以下步骤执行：

步骤一：令 x 的值为 n 除以 1000 的商，令 y 的值为 n 除以 1000 所得的余数；

步骤二：如果 x 大于 y，令 p 的值为 x – y，否则令 p 的值为 y – x；

步骤三：令 q 的值为 p 除以 7 所得的余数，输出 q，结束整个程序.

当输入 20222022 时，输出的值是多少？

答案：5

解析：20222022÷1000=20222...22,所以x=20222,y=22

20222＞22，p=20222-22=20200

20200÷7=2885...5

评析：2星  程序类问题

依葫芦画瓢即可

微信公众号搜索： 北京小学学习资料     家长升学指南   家长升学训练营  关注公众号，获取最新资讯！  

扫码添加“家长论坛”微信好友（微信号 16619908263）

获取华杯杯赛、华数之星、华罗庚金杯小中高组夏令营+冬令营+精英赛真题

咨询华杯杯赛、华数之星、华罗庚金杯政策请拨打电话 16619908263 （同微信号）