精选题-04|20年迎春杯大师赛构造题详细构造思路

点击领取>>>数学花园探秘总决赛暨迎春杯大师赛试题合集

模块：组合问题

难度：四星题

解题适用年级：四年级以上

来源：2020迎春杯大师赛六年级一试压轴

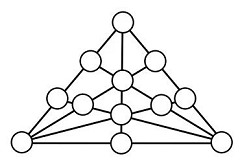
题目：如图，12个圆圈排在8条直线上，将12个连续的自然数分别填在12个圆圈中，再求出每条直线上所有圆圈所填数的和．

（1）试说明：不存在一种填法使这8个和都相等．

（2）是否存在一种填法，使得这8个和恰有2种不同取值？

       如果可以，请给出一种填法，如果不可以，请说明理由．

请先自行思考解答。思考时间：20分钟。

如果你是家长。也可以把题目抄写给小朋友。让他自行思考。不要着急看后面的解答。

◆  ◆  ◆

思考1：为方便表达，先将图中的12个圆圈标上字母。这是数阵图相关的题目，8条直线上的和是相等的（一般称之为幻和）。

第1种常见的思路是把所有的幻和都加一次看一下，每一个位置上的数算了几次。利用所有数都会出现，那么所有数的和与之对比，可能会有几个位置上的数有限制。但是8个幻和都加时，B、C算了4次，A、H、I算了3次，其它位置算了2次，总和减所有数2次，也会出现5个位置相关的限制，不方便讨论。

第2种就是选取部分的幻和和讨论，这里就要有一定的水平了。这一题能说明矛盾就行，那选取哪几条直线来讨论呢？

结合图形的对称性和特殊位置试试看吧

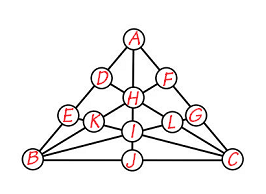
步骤1：

选取过B点的上面三条和过C点的上面三条。

①A+D+E+B,F+H+K+B,G+L+I+B

②A+F+G+C,D+H+L+C,E+K+I+C

这两组的总和都是3个幻和，其中A,D,E,F,H,K,G,L,I都算了一次，所以B=C,与题意矛盾。

思考2：这种两问的构造与论证的题目一般是一个可构一个不可构。直观的感觉，和取两种不同的值，调整的空间很大。但真去构造时，还是比较麻烦的。不妨从第一问当中，寻找一些思路。

在第1问的选择当中，关注到：A,D,E,F,H,K,G,L,I像是一个三阶幻方，类似点在于三行三列和是相等的。这样的话可以使得以B相关的其中三条和相等，与C相关的三条和相等，不过这两组和是不同的取值（B,C不同）。此时还剩两组和，AHIJ与BJC。我们的重点就是将AHIJ与BJC这两组和调整一下，使其与之前出现的两个值一样。

如何调整？

其中BJC这组只有三个数，其它和都有四个数，我们在满足其他组符合要求的情况下，可以通过将12个数同时加上相同的数，对应的差会变化。比如BJC的这组的和比其他的和少x，我们就将所有数都加x，就可以使8个和都相等了。不过如果我们第一次选择的数是最小的那几个自然数，就只能加，就是BJC的和要某个和大！

上面的想法，可让我们优选考虑AHIJ的和

首先要使得三阶幻方调整成A+H+I对角线和其它行列的和不一样，但配上J和B/C后要一样。

先来个常见幻方填法

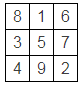
找一条对角线，调整一下，使对角线的和变化，且三行和三列的和还是相等，比如让一条对角线都加1：

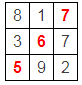
不过7又重复出现了，那把7变大1吧，但是其它数也要对应调整，要让三行三列的和一直都相等，可以把和另一个7不同行不同列的数，选两个。如：

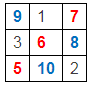
此时，我们要的对角线的和是5+6+7=18，三行和三列的3个数的和是9+1+7=17，不相等，18补上J要和17补B或C相等才行

这时只要让J比B或C小1就行。这个时候不要忘了12个连续自然数这个条件，所以必须多一个4。

可以这样让J=11,B=12,C=4

此时除了B+J+C=12+11+4=27

其它的和，要么是18+11=17+12=29，要么是17+4=21

用之前想到的思路，把此时的12个数每个数都增加了6，就会变成下图了

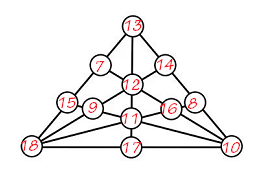
步骤2：可以，构造如图

◆  ◆  ◆

写在后面：还是要感谢和我一起讨论的老师同学和家长，欢迎所有人和我讨论漂亮的小奥题。

微信公众号搜索： 北京小学学习资料     家长升学指南   家长升学训练营  关注公众号，获取最新资讯！

扫码添加“家长论坛”微信好友（微信号 16619908263）

获取数学花园探秘总决赛暨迎春杯大师赛试题合集
咨询数学比赛/杯赛政策请拨打电话 16619908263 （同微信号）