北京小学奥数：神奇的连分数 1=2的诡证

连分数(continued fraction)是特殊繁分数，研究连分数的动机源于“实数”在“数学上纯粹”的表示：

如果a0，a1，a2，…an，…都是整数，则将分别称为无限连分数和有限连分数。例如：(假定a0为整数部分)

[a0；a1，a2，a3，a4……]

本期我们一起谈谈连分数的神奇之处。

每天叫醒你的不是闹钟，而是梦想和态度

难易指数：★★★★

适宜对象：小学培优

本期编号：D00064

关键词：一等于二、无限连分数、有限连分数

连分数

（1）有限连分数

所有有限连分数都表示一个有理数，而所有有理数都可以按两种不同的方式表示为有限连分数。这两种表示除了最终项之外都是一致的。在较长的连分数表示，其最终项是 1；较短的表示去掉了最后的 1，而向新的终项加 1。在短表示中的最终项因此大于 1，如果短表示至少有两项的话。

其符号表示：(a0代表整数部分)

[a0；a1，a2，a3，a4……]

要计算实数r的连分数表示，可先写下r的整数部分，然后从r减去这个整数部分。如果差为 0 则停止；否则找到这个差的倒数并重复。

例如：6.124，用连分数近似表示如下：

6.124-6=0.124

1÷0.124≈8.0645，8.0645-8=0.0645

1÷0.0645≈15.504，15.504-15=0.504

1÷0.504≈1.984，1.984-1=0.984

1÷0.984≈1.016，1.016-1=0.016

1÷0.016=62.5，62.5-62=0.5

1÷0.5=2，2-2=0.000（停止计算）

于是6.124用连分数就可以表示为：

数学上可表示整数序列为：

[6；8，15，1，1，62，2]

（2）无限连分数

所有无限连分数都是无理数，而所有无理数可用一种精确的方式表示为无限连分数。

无理数的无限连分数表示是非常有用的，因为它的初始段提供了对这个数的优异的有理数逼近。这些有理数可以叫做这个连分数的收敛（convergent，也译为“渐进”）。所有偶数编号的收敛都小于最初的数，而奇数编号的收敛都大于它。

π的其它表示方法：

黄金分割数φ= (√5+1)/2：

黄金比例相关的知识请参考：

D00042期：[分分钟涨知识]黄金比例

自然数e(欧拉数)：

自然数e相关的知识，请参考：

D00044期：欧拉数-自然常数e的来源及应用

其它：

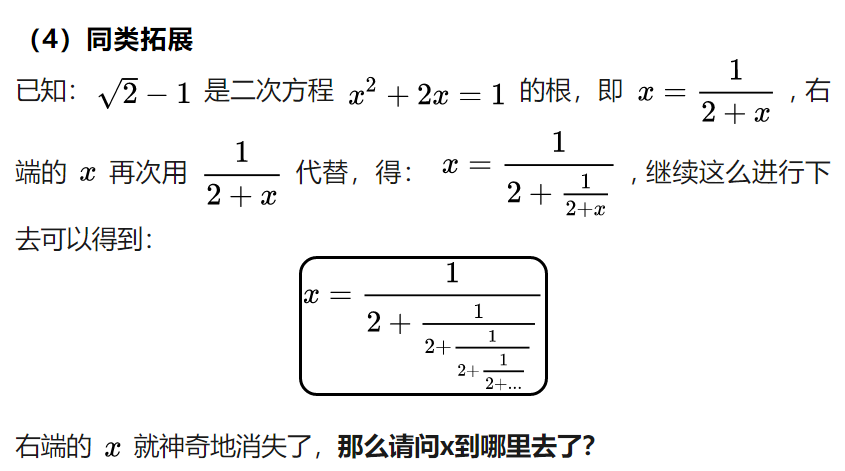
（3）1等于2的诡证

整数1可以用连分数表示如下：

无限的进行下去，于是可以得到1的连分数：

图“1”

整数2可以用连分数表示如下：

无限的进行下去，于是可以得到2的连分数：

图“2”

由图“1”、图“2”可以看出1=2，证毕。

那么请问，这个证明错在哪里呢？