第十八届沙雷金几何奥林匹克通讯赛

1.(8年级)外心为, 垂心为. 已知为的角平分线. 过作平行线与交于点. 求证: .

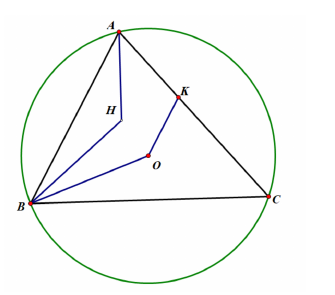
2.(8年级)四边形有内切圆, 圆心为,  分别为外心.
求证: 外心在角平分线上.

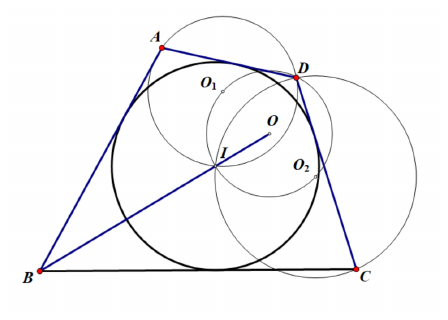
3.(8年级)直角中, , 为边上的高.作正和正, 其中和在 同侧, 在 同侧. 直线和交于点. 求证: .

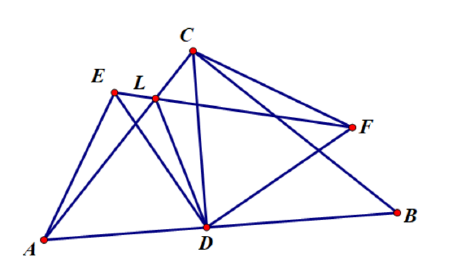
4.(8年级)的三条高分别为.  的内切圆边切于点. 类似的定义 . 求证:  三线共点.

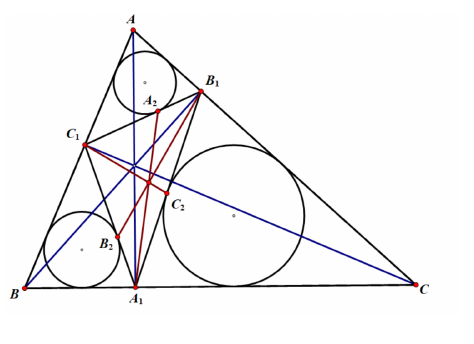
5.(8年级)圆内接四边形的对角线交于点. 过作的垂线与交于, 作的垂线与交于. 过作的外接圆的切线. 求证:与平行.

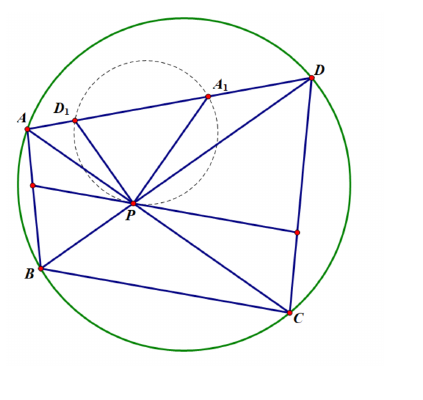
6.(8-9年级)的内切圆和B-旁切圆分别与边切于点. 直线分别和  的外接圆再次相交于. 求证: .

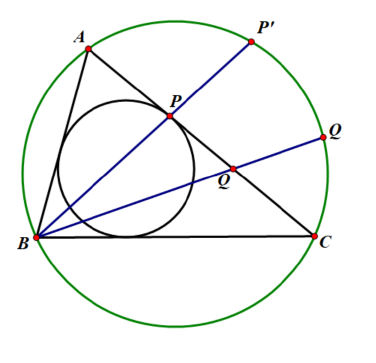
7.(8-9年级)对,以为边构造正方形, 作其中心. 取中点, 中点. 抹去除外的所有点和线. 请作出原.

8.(8-9年级)在三边上分别取点, 使得 设为外心, 为垂心. 求证: .

9.(8-9年级)四边形的内切圆与四边  , 分别切于点 , . 在直线上任取一点, 直线交于点, 直线交于点, 直线交于点,  求证: 共线.

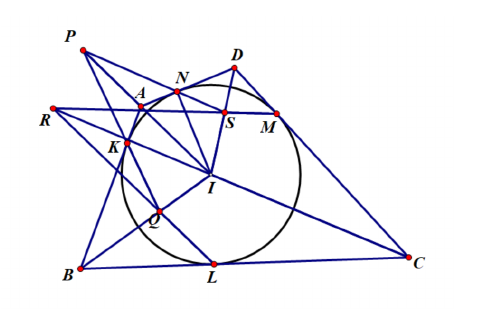
10.(8-9年级)外心为, 外接圆为. 圆与相切, 与的弧切于点. 设为内心. 求证: 垂直于的配位中线.

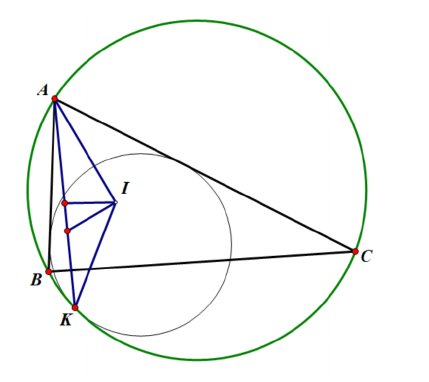
11.(8-10年级)中,  , 点满足   与 分别再次相交于点. 求证: 点到的距离相等.

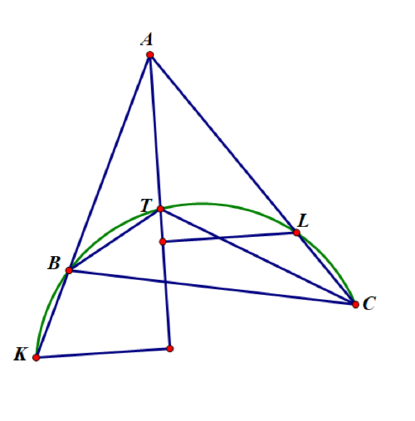
12.(8-11年级)凸四边形中, 分别为 中点. 线段,  的交点分别把它们分割为三个部分. 已知这三个部分中, 中间部分长度相对于线段总长度的比例为定值. 那么, 是否一定为平行四边形?

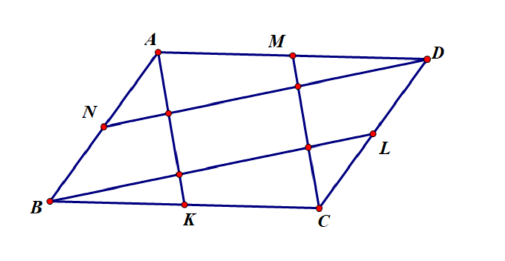
13.(8-11年级)给定平面上的八个点. 它们共组成个三角形. 将这些三角形的面积排成一行, 试证明, 可以在其中添加若干号或者号, 使得它们的和为.

14.在中,  和分别为边上的内切圆切点和边上的旁切圆切点. 类似的定义; .考虑的12条高的长度.
(8-9年级)求不同的长度个数的最大值;
(10-11年级)求不同的长度个数的所有可能值;

15.(9-11年级)在中, 为其内心, 平行于且与其内切圆相切的直线与其外接圆交于两点. 求证: .

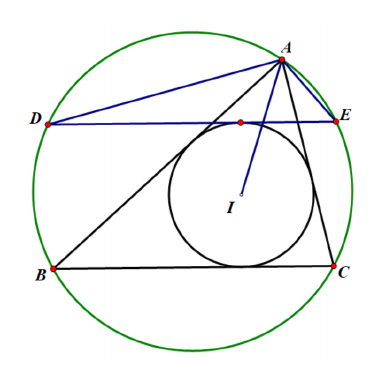
16.(9-11年级)圆内接四边形中,   若平分线与平分线分别与交于. 求证: 共圆.

17.(10-11年级)点为内部一点. 过作 的垂线, 分别与其外接圆交于点, . 证明: 若直线 , 均过点, 则满足条件的所有直线过一定点.

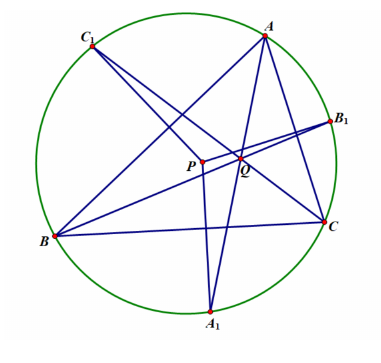
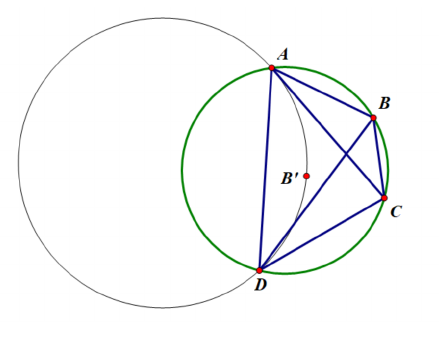
18.(10-11年级)圆内接四边形中, 对边相乘的乘积相等. 设为关于的对称点. 求证: 过的圆与相切.

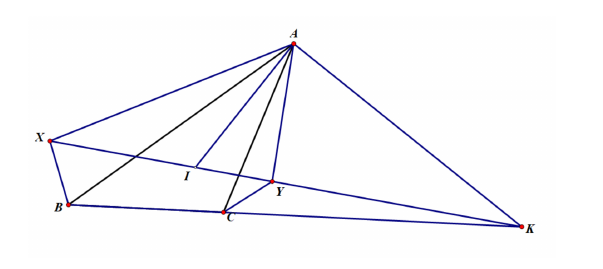
19.(10-11年级)设为内心, 为和的外角平分线的交点. 直线与的外角平分线分别交于点. 求证: .

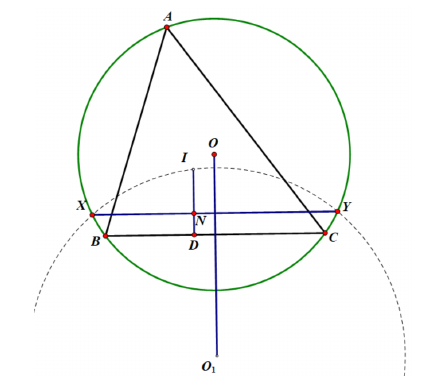
20.(10-11年级)设分别为外心和内心, 分别为其外接圆半径和内切圆半径. 为上的内切圆切点, 为上任意一点. 过作垂线与外接圆交于点. 设为圆心, 求.