小禾杯复赛完全平方数一题分析

模块：数论问题

难度：五星题

解题适用年级：五年级以上

来源：小禾杯复赛

题目： 使得1²，2²，…，n²的平均值是一个平方数的大于1的最小的正整数n等于______．

请先自行思考解答。思考时间：20分钟。

如果你是家长，可以把题目抄写给小朋友，让孩子自行思考。

◆  ◆  ◆

思考1：

由题意知

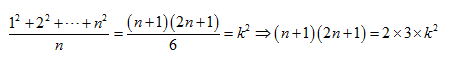
之后的过程就是对上面式子的讨论了~

怎么讨论呢？

式子中右边有6（2×3），结合完全平方数的性质

考虑左边质因数2和3的分布是一个不错的想法

2∤（2n+1），所以2∣n+1，得n是奇数

那么3呢，在两边除以6时，质因数3在哪个数中约了

（n+1）与（2n+1）能同时有3吗？

这个就可考虑两者间的关系了

这两个数是互质的，理由可用辗转相减法证最大公因数是1

（n+1，2n+1）=（n，n+1）=（1，n）=1

这个时候就有两者情况：

①3∣（n+1），3∤（2n+1）

②3∣（2n+1），3∤（n+1）

逐一考虑吧

①当3∣（n+1）时，就是（n+1）/6与（2n+1）互质，且乘积是完平

那么它们分别都是完平

（n+1）/6=a²,（2n+1）=b²

有没有可能呢，这个时候就要从完平的一些性质来分析了

b²=2n+1，奇数完平，可以考虑除以4的余数

因为n是奇数，所以2n+1除以4余3，但完平除以4只能余0或1

所以矛盾

②3∣2n+1，3∤n+1

题目就转化为（n+1）/2=a²,（2n+1）/3=b²，找到n>1的最小值

思考2：

如果没有更好的办法，可以用n是奇数，这个条件，限制出b²是一个奇数，用奇完平从小到大枚举也是可以完成的。

但这里不妨再对这两个完平做更细致的讨论

比如a²与b²的关系式可以先整理出来

4a²=3b²+1

再考虑a²与b²的限制

比如是否含2或3这类

这里给一个方向：

a²是否还含有质因数2

若a²含有2

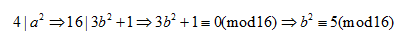
矛盾

所以a²不含有2，a²除以4只能余1，

4a²就是一个除以16余4的数

即：

用这个限制从小到大去验证，当b=15时，a=13，等式成立。

此时n=337

微信公众号搜索： 北京小学学习资料     家长升学指南  关注公众号，获取最新资讯！   

扫码添加“家长论坛”微信好友（微信号 16619908263）

获取历年小禾杯数学竞赛初试复试真题试卷及答案
咨询小禾杯数学竞赛初试复试政策请拨打电话 16619908263 （同微信号）