[ 数学 ] 第25届YMO交流活动小学5年级初赛试题

点击领取>>>YMO世界青少年奥林匹克数学竞赛选拔赛决赛试卷题

一、选择题.（每题 4 分，共 40 分）❝

1、在所有的质数中，偶数的个数（   ）。

A. 只有一个

B. 有两个

C. 有三个

D. 有无数个

❞

「答案解析」

2既是偶数又是质数，特别要注意2的特殊性，在和质数相关的题目中，很多都和2相关。

选A。

❝

2、 的分母加上9，要使分数的大小不变，分子应加上（   ）。

A. 9

B. 7

C. 14

D. 21

❞

「答案解析」

不用真的去算，分母扩大了3倍，那分子也扩大3倍即可，因此，分子要加上21。

选D。

❝

3、等边三角形形有（   ）条对称轴.

A. 1

B. 2

C. 3

D. 4

❞

「答案解析」

每条边上的高所在的直线就是对称轴。

选C。

❝

4、a 与 b 是互质数，它们的最小公倍数是最大公因数的（   ）倍。

A. 1

B. a

C. b

D. ab

❞

「答案解析」

两个互质数的最大公因数是1，最小公倍数就是ab。

选D。

❝

5、一个三角形，三个内角度数的比为，则此三角形为（   ）三角形。

A. 锐角

B. 直角

C. 钝角

D. 无法确定

❞

「答案解析」

注意到，因此有一个角比直角大。

选C。

❝

6、在一个正方形里面画一个最大的圆，圆的面积是正方形面积的（   ）。

A.  

B.  

C.  

D.  

❞

「答案解析」

设圆的半径为1，则其面积为，则满足题意的正方形的边长为2，则其面积为4。

因此，选D。

❝

7、 用两个质数之和来表示 100 有许多种方法，在这些方法中，两个质数的乘积最大是（  ）。

A. 2491

B. 2499

C. 2500

D. 2419

❞

「答案解析」

两个质数的和是100，要想让其质数的乘积最大，则这两个质数的差要尽可能小。

因此，一个质数要大于50，另一个质数要小于50，在脑袋里遍历下质数表，满足要求的两个质数就是53和47，其乘积为2491。

选A。

❝

8、 定义 （），在 、、、...、中划去一个，剩余的数的乘积是一个完全平方数，划掉的是（   ）。

A. 24！或 25！

B. 25！

C. 26！

D. 25！或 26!

❞

「答案解析」

在 、、、...、  这50个阶乘的乘积中，1乘了50次，2乘了49次，3乘了48次，依此类推，可以发现任意一个奇数的个数都是偶数个，任意一个偶数的个数都是奇数个。

我们知道，某一个数乘以偶数次，其积一定是个平方数。

我们记：

其实等价于：

我们先将偶数次方全写在一起，：

可以判定，此道题出错了，划掉一个是不可能的。

因为25是一个平方数，正确答案应该是划掉和，或者划掉和。

因此，猜测出题者的本意是划掉或者，但考虑不周，导致答案错误。

如果非要选，就选A这个错误答案。

❝

9、 任意连续 n 个非 0 自然数，有（ ）个是 n 的倍数。

A. 0

B. 1

C. 1 或 2

D. 不确定

❞

「答案解析」

连续n个非0自然数，那这个，那么我们举些特例，譬如，或者，可以看到，每组里只有一个是4的倍数。

选B。

❝

10、 一个大正方体，切割成 n 个小正方体后，表面积增加了 4 倍，则 n 是（ ）。

A. 27

B. 64

C. 125

D. 216

❞

「答案解析」

因为大立方体均分成形状一样的小立方体，其数量肯定是一个立方数。

为了计算简单些，我们将题目改下，假设是切割成个小正方体。

设小正方体的变成为1，那每个小正方体的表面积就是6，所有小正方体的表面积为。

那么，大正方体的边长为，则其表面积为。

因此，有：

也就是：

所以，，那。

如果不用方程的思维，经过推导，我们一定要明白，切割后的表面积变成了原来的n倍，但却只是增加了4倍，那么。

再变换回去，那么就选C。

二、填空题（每题 4 分，共 60 分）❝

1、 分母不大于60，并且分子小于 6 的的最简真分数有（ ）个。

❞

「答案解析」

这种题目用分类汇总法来计算。

不大于60，是包括60的。

当分子为1的时候，分母可以从2到60，共有59种最简真分数。

当分子为2的时候，我们去掉60以内的偶数和1，共有29种最简真分数。

当分子为3的时候，3的倍数共有20个，最简真分数有 个。

当分子为4的时候，由于是求最简分数，那分母肯定不能是偶数，最简真分数有个

当分子为5的时候，5的倍数共有12个，最简真分数有个。

因此，满足条件的最简真分数有个。

此类题目很容易通过程序去验证：

#include <iostream>
using namespace std;

//辗转相除法求最大公因数
int gcd(int m,int n){
 if(n==0)return m;
 else return gcd(n,m%n);
}

int main(){
 int a,b,num=0,c;
 
 
 for(a=1;a<6;a++){
  c=0;
  for(b=a+1;b<61;b++){
   if(a==1||gcd(a,b)==1){
    cout<<a<<"/"<<b<<" ";
    if((c+1)%10==0)cout<<endl;
                c++;
   }
  }
  cout<<endl<<"分子为"<<a<<"的真分数有"<<c<<"个。"<<endl<<endl;
  num+=c;
 }
 
 cout<< "满足条件的真分数一共有"<<num<<"个。";
 return 0;
}

输出如下：

1/2 1/3 1/4 1/5 1/6 1/7 1/8 1/9 1/10 1/11
1/12 1/13 1/14 1/15 1/16 1/17 1/18 1/19 1/20 1/21
1/22 1/23 1/24 1/25 1/26 1/27 1/28 1/29 1/30 1/31
1/32 1/33 1/34 1/35 1/36 1/37 1/38 1/39 1/40 1/41
1/42 1/43 1/44 1/45 1/46 1/47 1/48 1/49 1/50 1/51
1/52 1/53 1/54 1/55 1/56 1/57 1/58 1/59 1/60
分子为1的真分数有59个。
    
2/3 2/5 2/7 2/9 2/11 2/13 2/15 2/17 2/19 2/21
2/23 2/25 2/27 2/29 2/31 2/33 2/35 2/37 2/39 2/41
2/43 2/45 2/47 2/49 2/51 2/53 2/55 2/57 2/59
分子为2的真分数有29个。
    
3/4 3/5 3/7 3/8 3/10 3/11 3/13 3/14 3/16 3/17
3/19 3/20 3/22 3/23 3/25 3/26 3/28 3/29 3/31 3/32
3/34 3/35 3/37 3/38 3/40 3/41 3/43 3/44 3/46 3/47
3/49 3/50 3/52 3/53 3/55 3/56 3/58 3/59
分子为3的真分数有38个。
    
4/5 4/7 4/9 4/11 4/13 4/15 4/17 4/19 4/21 4/23
4/25 4/27 4/29 4/31 4/33 4/35 4/37 4/39 4/41 4/43
4/45 4/47 4/49 4/51 4/53 4/55 4/57 4/59
分子为4的真分数有28个。
    
5/6 5/7 5/8 5/9 5/11 5/12 5/13 5/14 5/16 5/17
5/18 5/19 5/21 5/22 5/23 5/24 5/26 5/27 5/28 5/29
5/31 5/32 5/33 5/34 5/36 5/37 5/38 5/39 5/41 5/42
5/43 5/44 5/46 5/47 5/48 5/49 5/51 5/52 5/53 5/54
5/56 5/57 5/58 5/59
分子为5的真分数有44个。
    
满足条件的真分数一共有198个。
❝

2、 有若干人去打猎，平均 6 人猎得 5 只野兔，15 人猎得 2 只鹿，10 人猎得 1 只野猪，结果最后每人分得一只猎物，还剩 4 只猎物。参加打猎的有（ ）人。

❞

「答案解析」

不知道怎么做，那就只好设未知数了。

假设有x人，则有如下方程：

也就是：

解得

❝

3、 YMO 数学竞赛，满分是 100 分，某小组的 8 位同学的得分都是整数，并且互不相同。已知这 8 位同学的平均分是 91 分，其中一位同学仅得 74 分，那么排在第五名的同学至少得（  ）分。

❞

「答案解析」

小组8人的总分是

去掉得分为74的同学，则其他七人的总分为：

其余7人的平均分为：

按题目的意思，要求排名第五的同学得分的最小值，那前面排名前四的同学的得分必须尽可能高，而且各不相同。

那么，我们假设前四名的得分和是：

那剩下的三人的得分必须达到：

因此，这三人得分的平均数是：

那么，要想第五名得分最小，那么此三人的分数必须尽可能接近，那么只能是：

因此，排名第五的同学得分至少是分。

我们反过来验证一下，只要前四名的同学得分小于分，那么排名第五的得分就会超过分。

❝

4、 李叔叔从果园摘了 30个苹果，按大小分成一等品 10 个，二等品 20 个。后来将一等品中最小的 3 个调整为二等品，这样使二等品苹果的平均质量提高了 20 克，一等品苹果的平均质量提高了 8 克。那么原来一等品苹果的平均质量比二等品的平均质量多（ ）克。

❞

「答案解析」

此类问题，想不明白就可以画个图来帮助我们想。

可以看到，将3个最小的一等品放到二等品中，二等品平均质量提升了20克，那么，提升的总质量就是：

也就是说，这400克是从3个最小的一等品里匀出来分给其他20个二等品的。

同时，拿掉3个最小的一等品，一等品的平均质量提升了8克，这句话的意思是，加入三个较小的一等品，原来7个一等品的质量平均下降了8克，那么7个一等品下降的总质量是：

也就是说，这56克是从7个一等品中匀出来分给这3个较小的一等品的。

因此，一等品原有的平均值比二等品新的平均值高出的质量为：

因此，原有一等品的均值比原有二等品均值高出的质量为：

❝

5、 两个连续奇数的乘积是 3599，那么这两个奇数的和是（ ）。

❞

「答案解析」

此类题目我们可以设未知数，

也可以分解质因数，但这个数比较大，如果尝试了几个质数还不行就建议放弃。

如果设未知数，那么我们分别设这两个连续奇数为和，

那么就有：

利用平方差公式去掉括号，如果不会平方差的话，我们就老老实实地展开计算，可以得到：

也就是：

因此，

这两个奇数的和就是

其实，这道题我们也可从末位数的特征入手，连续的两个奇数相乘末位是9，那么这两个奇数的末位数必须是9和1了，然后连续两个奇数的乘积又接近于一个平方数，那么这个平方数只能是3600了。

❝

6、 如果 6 位数20□□20能被 105 整除，那么这个 6 位数最大是（ ）。

❞

「答案解析」

由于

所以，该数必须是3的倍数，也是7的倍数，由于末尾是0，也必然是5的倍数。

其实我们可以根据质数的特征来尝试下，在判断是7的倍数时，我们可以采取三位截断法，奇偶段相减的方法来判断。但该数比较大，计算的时候也不太方便。

所以，我们可以先假设中间的两位数为，那么：

也就是

同理，

也就是：

现在就柳暗花明了，必有：

所以：

由于是一个最大的两位数，我们取，此时。

❝

7、 如果一个自然数的因数的个数是奇数，我们称这个自然数为“YMO 数”。那么，小于 1000 的最大的“YMO 数”是（ ）。

❞

「答案解析」

一个数如果能分解质因数，那么必然能分解成的形式，此时就有两个因数，如果还能继续分解，那么因数的个数似乎总会是偶数个。

什么情况下，因数的个数是奇数个呢？

很明显，当一个数是平方数的时候，无论进行多少次分解，总会出现，此时只能算一个因数。因此，平方数的因数的个数总是奇数。

那么，1000以内的平方数，最大的就是。

❝

8、 用 1 至 9 这 9 个数字各一次，组成一个两位完全平方数，一个三位完全平方数，一个四位完全平方数。那么，其中的四位完全平方数最小是（ ）。

❞

「答案解析」

看到这样的题目，是不是有无从下手的感觉呢？

既然要求四位的完全平方数最小，我们先大胆地猜测下这样的四位数的千位是1。

那么，2000以内的完全平方数有哪些呢？由于，那么应该是从到吧？

我们先将这些平方数全部列出来，考虑到数字的不可重复，也不能包含0，

那么，我们可以拿到的满足要求的四位平方数有：

（1）我们先考虑1296，那么剩下的五个数字是：

我们注意到平方数的末位数只能是：

那么，在剩下的五个数字中，满足条件的两位数25和64都不存在。

（2）我们再考虑1369，那么剩下的五个数字是：

考虑到平方数的末尾特征，那么两位平方数只能是25，那剩下的874或784会是平方数吗？

经过验证，我们确认

因此，满足要求的最小的四位平方数是1369。

这样也比较幸运，幸好1开头的四位数有满足要求的，否则下一轮从2开头的四位数继续算。

我们也可以编写程序来列举满足要求的平方数，代码如下：

#!/usr/bin/env python

two=[x*x for x in range(4,10)]
three=[x*x for x in range(11,32)]
four=[x*x for x in range(33,100)]

for i in two:
    for j in three:
        for k in four:
            a=[]
            n=[i,j,k]
            for x in n:
                for t in range(4):
                    g=x//pow(10,t)%10
                    if g>0 and g not in a:
                        a.append(g)
            
            if len(a)==9:
                print(i,j,k)

可以找到满足要求的数有：

16 784 5329
25 784 1369
25 784 1936
25 841 7396
36 729 5184
81 324 7569
81 576 3249
81 729 4356
❝

9、 s= ，求s。

❞

「答案解析」

每项分数都很有规律，可以通过裂项求和法来做。

所以：

消去相邻项目，得到：

❝

10、 张、王、李三户人家打算订阅报纸，共有 8 种不同的报纸可供选择，已知每户人家都订三份不同的报纸，并且知道这三户人家每两户所订的报纸都恰好有一份相同，那么三户人家共有（   ）种不同的订阅方式。

❞

「答案解析」

此类排列组合题还是比较麻烦的，麻烦就在于要考虑到多种可能性，然后再汇总。

记得排列组合应该是高中才学的内容吧，怎么跑到小学的竞赛里来了？

（1）我们先考虑第一种情况。三户人家挑选的报纸，有一种是相同的。

那么这份共同订阅的报纸是从8种里选一种，那就有种选法，张家从剩下的7种里挑2种，就是，王家从剩下的5种里挑2种，就是，李家从剩下的3种里挑2种，就是，不同的订阅方式就是：

（2）我们再考虑第二种情况。用不同的字母代表一种报纸，那这种情况可以描述成，那两两相同的报纸只有三种，需要从8种报纸里任取3种，这是一个排列问题，然后从所挑出的3个里再无序选择2个，这是一个组合问题，最后剩下的，又是一个排列问题，需要再从剩下的5种里任取3种。

因此，三户人家共有：

种订阅方式。

❝

11、 如下图，直角三角形 ABC 中，BC=18，AC=24，将 AC 对折到斜边 AC 上，使 AC 与 AD 重合，则三角形 BDE 的面积是（   ）。

❞

「答案解析」

难道小学就要用勾股定理或者三角形相似了吗？

很多小朋友虽然没学过勾股定理，但一定听说过直角三角形里的"勾三股四弦五"的事情吧。

可以看到，直角三角形的一个直角边是6个勾三，另一个直角边是6个股四，那斜边就是6个弦五，斜边AB的长度也就是30。

我们设CE的长度为a，BD的长度为b，那么DE的长度也是a，AD的长度为24，线段DE垂直于线段AB于点D。

因此，b就等于：

根据面积关系，有：

也就是：

从而解得。

或者根据三角形相似，对应边的比例是相等的，有：

也可以解得和。

从而可得阴影部分的面积为

❝

12、 在下面的算式中，不同汉字代表 0-9 不同的数字。如果“学=5”，那么“素质赛”是（ ）。

青少年素质赛品学兼优❞

「答案解析」

先将2020分解下质因数，可以看到：

由于汉字代表的是不同的数字，所以"素质赛"不可能是101及其倍数。

所以：

品学兼优

既然"学"是5，那么"优"就是6。

因此，"品"和"兼"要么是2和7，要么是1和8，不能是0和9。

我们先考虑第一种情况，"品"和"兼"是2和7，

那么，我们就要从0、1、3、4、8、9中挑出数来，满足：

青少年素质赛

很明显，"青"不能是0，"年"也不能是0，那么，只能"赛"是0，

素质少年青

通过观察，

等"青"等于1的时候，"素质"可以是38，"少年"可以是19，冲突。

当"青"等于4的时候，"少年"等于38，"素质"等于19，此时满足要求。

也就是：

成立。

因此，"素质赛"可以是190。

我们再考虑第二种情况，"品"和"兼"是1和8，同理，"赛"只能是0，

那么，我们就要从2、3、4、7、9中挑出数来，满足：

素质少年青

很明显，当"青"等于2或4时，无解，其他情况更不可能。

❝

13、 如下图，正六边形面积为 18 平方厘米，那么阴影部分面积是（ ）平方 厘米。

❞

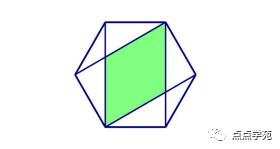
「答案解析」

要想算出来，也得用到初中的数学知识，只是正六边形的边长为，这个不大好计算。

不过在这里是填空题，我们可以投机取下巧。

如下图所示，我们将其他的辅助线都加上，可以看到该图形对称轴很多，基于中心点O旋转，基本上都是可以重叠的。

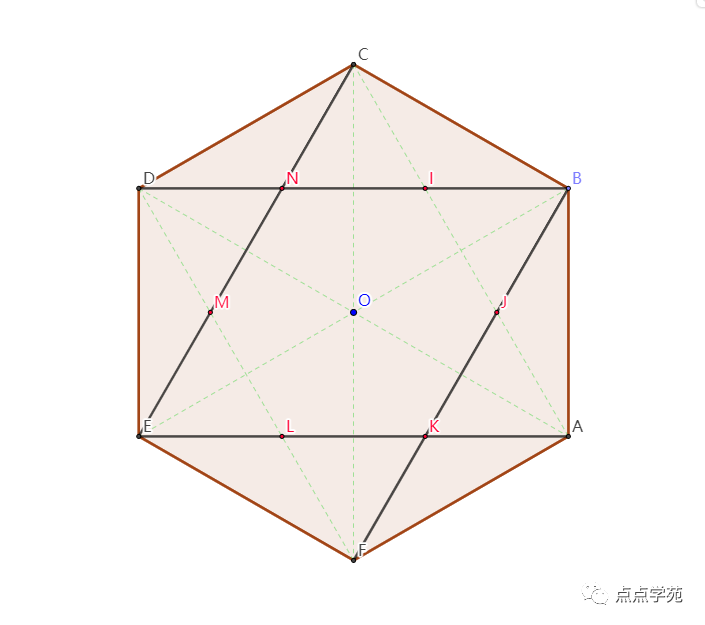
因此，正六边形被均匀分成6个全等的等边三角形，每个的面积为。

同时，等腰三角形等几个三角形，每个的面积也为3。

同时，线段BD被点N和I三等分，线段CE、AE和BF也一样，

因此，，

所以，阴影部分的面积就是。

❝

14、 如下图，在三角形 ABC 中，点 D 是 AC 的中点，点 E、F 是 BC 的三等分点， 若三角形 ABC 的面积是 60 平方厘米，则四边形 CDMF 的面积是（   ）平方厘米。

❞

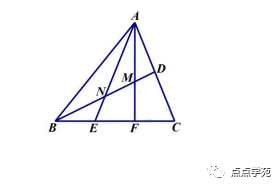
「答案解析」

我们首先重画下示意图，连接CM，连接EM。

将三角形ADM的面积标注为S1，将三角形CDM的面积标注为S3，将三角形CDM的面积标注为S2。

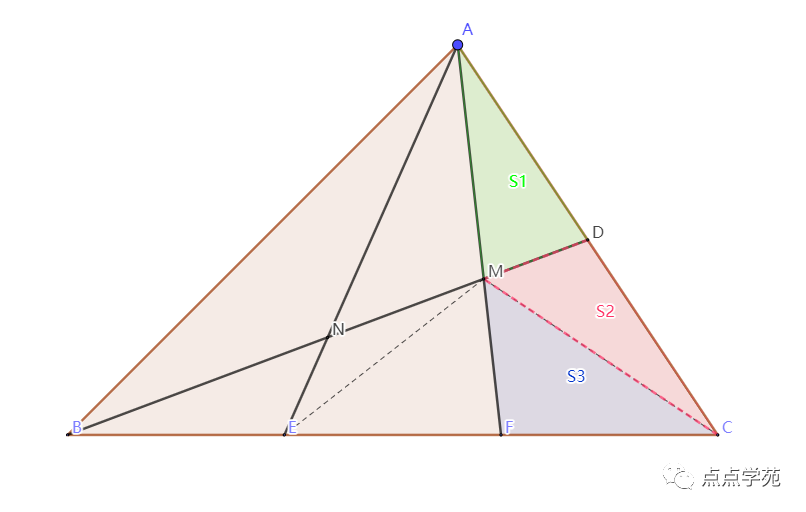
从而有如下关系：

从而可以解得：

从而，四边形CDMF的面积就是：

初中如果学了梅涅劳斯定理，或者做平行线，也可以比较轻松地解答出来。

这里我们先用梅涅劳斯定理来求下线段之间的比例关系，得到这些比例关系后，三角形的面积关系也就可以轻易地求出来。

直线BD穿过三角形AFC，分别于三条边相交于B、M、D三点，有：

因此，可以得到：

所以：

又因为：

所以，，。

所以，，

所以，。

同理，再应用一遍梅氏定理，可以得到，从而可以将其他四块区域的面积都求出来。

譬如：，，，。

❝

15、小明骑自行车从甲地到乙地，要先骑一段上坡路，再骑一段平坦路。他到乙地后， 立即返回甲地，来回共用了 3 小时。小明在平坦路上比上坡路每小时多骑 10 千米，下坡路比平坦路每小时多骑 5 千米。还知道他在第 1 小时比第 2 小时少骑 8 千米， 第 2 小时骑了一段上坡路，又骑了一段平坦路，第 2 小时比第 3 小时少骑了 5 千米。甲乙两地之间的距离是（    ）千米。

❞

「答案解析」

被这题目搞得晕头转向的，一定要画好示意图。这样的题目，如果用常规的路程问题来解，那变量就太多了，解答起来很麻烦。

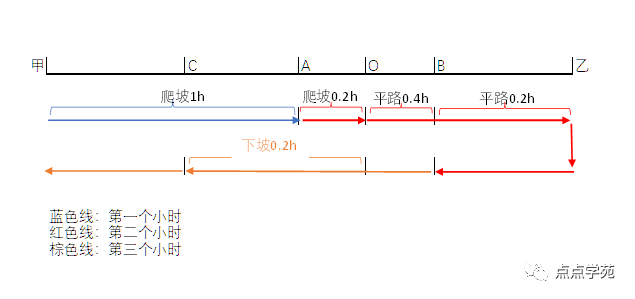
从示意图可以看到，小明从甲爬坡到A点，花了1个小时。

从A点到O点继续爬坡，过了O点后走平路到乙点后返回，到B点后又花了1个小时。

从B点继续走了一段平路，然后从O点开始下坡，返回甲地，又花了1个小时。

这里我们要搞清楚，第2小时为什么会比第1小时多跑了8公里呢？

AO段是在爬坡，速度跟第1小时一致，因此，多跑的8公里是甲到达O地后，1小时内剩下的时间拉出来的差距。

假设在平路骑行的速度是v，因此，小明从O地到乙，然后再返回B地，所耗费的时间就是：

也就是说，第2个小时里，有0.8小时走的是平路。

因此，小明从A地到O地，所耗费的时间就是：

同理，返回时小明从B骑行到O地，速度和平地一致，没有拉开差距。

小明上坡时，从A地到O地花了0.2小时，那么在这么长的时间内，小明下坡可以拉开的距离是：

那么，剩下的公里的距离，是其他下坡时间跟走平路拉开的，因此，这段走平路所花的时间为：

也就是说，从B地到乙地，再从乙地到B地，所花的时间就是0.4小时。

因此，小明从乙地骑行到B地，花的时间就是：

所以，小明从O地到B地，花的时间就是：

因此，从甲地到O地的上坡路程就是：

同理，从O地到甲地的下坡路程，用返程的速度和时间表达出来就是：

由于距离相等，有：

可以解得:

从而，甲乙两地的距离就是：

微信公众号搜索： 北京小学学习资料     家长升学指南  关注公众号，获取最新资讯！

扫码添加“家长论坛”微信好友（微信号 16619908263）

获取YMO世界青少年奥林匹克数学竞赛选拔赛决赛试卷真题
咨询YMO世界青少年奥林匹克数学竞赛政策请拨打电话 16619908263 （同微信号）