[数学]第29届YMO交流活动小学6年级初赛试题

点击领取>>>YMO世界青少年奥林匹克数学竞赛选拔赛决赛试卷题

1、比（）千克多35%是27千克。

「答案解析」

将原有的看作是1，则原有的1.35倍等价于27千克，因此，原有的就是：

2、一个圆锥与一个圆柱的底面积相等，已知圆锥与圆柱的体积之比是1:6，圆锥的高是4.5厘米，则圆柱的高是（ ）厘米。

「答案解析」

同底等高的圆锥和圆柱的体积比是1:3，根据条件，说明圆柱的高是圆锥的两倍，因此，圆锥的高是9厘米。

3、用1、2、3、4、5、6能组成（  ）个同时能倍2和3整除，且十位数字与个位数字相同的三位数。

「答案解析」

数字较少，我们可以用枚举法。

能被2整除，说明末位上的数字只能是偶数2、4和6。

当末位数是2的时候，只能有222和522两个。

当末位数是4的时候，只能有144、444两个。

当末位数是6的时候，只能有366、666两个。

所以，这样的三位数共6个。

4、六年级四个班共订某种课外读物100本，每个班至少订24本，至多订27本，则有（  ）种不同的订法。

「答案解析」

无论怎么样，按题目要求，100本课外读物只能分解成下面这样的四种订法：

考虑第(1)种情况，相等的情况出现了2次，订法是：

考虑第(2)种情况，相等的情况出现了1次，订法是：

考虑第(3)种情况，相等的情况出现了3次，订法是：

考虑第(4)种情况，相等的情况出现了1次，订法是：

一共是:

种。

5、某些数除以11余1，除以13余3，除以15余14，那么这些数中最小的数是（  ）。

「答案解析」

中国剩余定理的简单应用，虽然不记得其公式，但如果我们能记得其思想，或者记住那句歌谣，那也比较容易计算。

对小学生来说，一般已经是对问题做了简化，我们设该数是x，则可列出方程来死算。

仔细观察，发现如果将x增加10以后，刚好能同时被11和13整除，因此有：

也就是:

所以有：

也就是：

所以，取时满足要求。

所以，，此时。

如果根据中国剩余定理，这个的最小解就是：

其中a、b、c都是模中的逆运算。

说起这逆运算，这些抽象概念可能有点难理解，其实我们也不需要关心。从本质上来说，我们就是要找出任意一个合适的a、b、c，也就是求：

这个就比较容易，任意一个满足条件的解都行，

可以求得，，，代入前面的式子，

大家分别用其取去除11、13和15，看看余数是不是和题目里的要求所匹配。

再对取模，就可以得到最小数是419。

请大家仔细琢磨编者前面列举的那个长算式，如果理解了其中的思想，中国剩余定理的原理也就明白了，以后应付此类问题轻而易举。

6、加工一个零件，甲要9分钟，乙要12分钟，丙要15分钟。现有423个零件，甲乙丙三人一起完成，乙需要加工（  ）个零件。

「答案解析」

甲乙丙三人一起工作时，需要的时间为：

因此，乙需要加工的零件是：

7、有一块长方形铁皮，剪下两段两个圆及中间剩下的长方形，刚好可以做成一个圆柱体，这个圆柱体的底面半径是7厘米，那么圆柱体的体积是（  ）立方厘米。（圆周率取3）

「答案解析」

剩下的长方形的底面长就是圆柱体底面周长，圆柱体的高就是底面的直径。

体积就是：

8、一根绳子，第一次剪去全长的，第二次剪去余下部分的，两次剪去的部分比余下的部分多3米，则这根绳子原来长（  ）米。

「答案解析」

第一次剪去，第二次剪去，两次剪去了：

所以，绳子长为：

9、某工厂生产的灯泡中有是次品，实际检查时，只发现其中的被剔除，另有的正品也被误以为是次品而被剔除，其余灯泡全部上市出售，那么该工厂出售的灯泡中次品所占的百分比是（  ）%。

「答案解析」

假设工厂生产的灯泡有100个，那么其中20个是次品，但只有个被剔除，那么保留了留下了个次品。

同时，还有个正品也被剔除了。

所以，总共被剔除的产品有个，拿来销售的灯泡共有个，其中次品4个，所求次品率就是：

也就是5%。

1、比（）千克多35%是27千克。

「答案解析」

将原有的看作是1，则原有的1.35倍等价于27千克，因此，原有的就是：

2、一个圆锥与一个圆柱的底面积相等，已知圆锥与圆柱的体积之比是1:6，圆锥的高是4.5厘米，则圆柱的高是（ ）厘米。

「答案解析」

同底等高的圆锥和圆柱的体积比是1:3，根据条件，说明圆柱的高是圆锥的两倍，因此，圆锥的高是9厘米。

3、用1、2、3、4、5、6能组成（  ）个同时能倍2和3整除，且十位数字与个位数字相同的三位数。

「答案解析」

数字较少，我们可以用枚举法。

能被2整除，说明末位上的数字只能是偶数2、4和6。

当末位数是2的时候，只能有222和522两个。

当末位数是4的时候，只能有144、444两个。

当末位数是6的时候，只能有366、666两个。

所以，这样的三位数共6个。

4、六年级四个班共订某种课外读物100本，每个班至少订24本，至多订27本，则有（  ）种不同的订法。

「答案解析」

无论怎么样，按题目要求，100本课外读物只能分解成下面这样的四种订法：

考虑第(1)种情况，相等的情况出现了2次，订法是：

考虑第(2)种情况，相等的情况出现了1次，订法是：

考虑第(3)种情况，相等的情况出现了3次，订法是：

考虑第(4)种情况，相等的情况出现了1次，订法是：

一共是:

种。

5、某些数除以11余1，除以13余3，除以15余14，那么这些数中最小的数是（  ）。

「答案解析」

中国剩余定理的简单应用，虽然不记得其公式，但如果我们能记得其思想，或者记住那句歌谣，那也比较容易计算。

对小学生来说，一般已经是对问题做了简化，我们设该数是x，则可列出方程来死算。

仔细观察，发现如果将x增加10以后，刚好能同时被11和13整除，因此有：

也就是:

所以有：

也就是：

所以，取时满足要求。

所以，，此时。

如果根据中国剩余定理，这个的最小解就是：

其中a、b、c都是模中的逆运算。

说起这逆运算，这些抽象概念可能有点难理解，其实我们也不需要关心。从本质上来说，我们就是要找出任意一个合适的a、b、c，也就是求：

这个就比较容易，任意一个满足条件的解都行，

可以求得，，，代入前面的式子，

大家分别用其取去除11、13和15，看看余数是不是和题目里的要求所匹配。

再对取模，就可以得到最小数是419。

请大家仔细琢磨编者前面列举的那个长算式，如果理解了其中的思想，中国剩余定理的原理也就明白了，以后应付此类问题轻而易举。

6、加工一个零件，甲要9分钟，乙要12分钟，丙要15分钟。现有423个零件，甲乙丙三人一起完成，乙需要加工（  ）个零件。

「答案解析」

甲乙丙三人一起工作时，需要的时间为：

因此，乙需要加工的零件是：

7、有一块长方形铁皮，剪下两段两个圆及中间剩下的长方形，刚好可以做成一个圆柱体，这个圆柱体的底面半径是7厘米，那么圆柱体的体积是（  ）立方厘米。（圆周率取3）

「答案解析」

剩下的长方形的底面长就是圆柱体底面周长，圆柱体的高就是底面的直径。

体积就是：

8、一根绳子，第一次剪去全长的，第二次剪去余下部分的，两次剪去的部分比余下的部分多3米，则这根绳子原来长（  ）米。

「答案解析」

第一次剪去，第二次剪去，两次剪去了：

所以，绳子长为：

9、某工厂生产的灯泡中有是次品，实际检查时，只发现其中的被剔除，另有的正品也被误以为是次品而被剔除，其余灯泡全部上市出售，那么该工厂出售的灯泡中次品所占的百分比是（  ）%。

「答案解析」

假设工厂生产的灯泡有100个，那么其中20个是次品，但只有个被剔除，那么保留了留下了个次品。

同时，还有个正品也被剔除了。

所以，总共被剔除的产品有个，拿来销售的灯泡共有个，其中次品4个，所求次品率就是：

也就是5%。

10、小明所在的学校合唱团有学生72人，其中女生占全体的37.5%，后来又增加女生若干人，这时女生人数恰好是全合唱团人数的40%，那么又增加了（  ）名女生。

「答案解析」

我们考虑不变的男生。

男生人数是：

那后来的总人数就是：

那增加的女生数就是：

11、所有运动员分成三个组，男女运动员的总数之比为4:3，第一组中男女人数比为6:5，第二组中男女人数比为3:5，且第一、第二、第三组的人数之比为11:16:9，第三组中男女人数比值是(   )。

「答案解析」

设第一组人数为，第二组人数为，第三组人数为，

则第一组中男生为，女生为，则第二组中男生为，女生为。

设第三组中男女比例为，则有：

也就是：

从而：

所以：

12、一水池装有两个相同的进水管和一个排水管，如果只开1个排水管，6小时可将一池子水排空;如果开1个进水管和1个排水管，3小时可以将空池灌满，现在将2个进水管和1个排水管同时打开，那么( )分钟可以灌满水池的一半。

「答案解析」

排水管的效率是，则进水管的效率是：

那么，灌满一般池水需要的时间是：

13、采购甲、乙、丙三种糖果，三种的购买总价比为3:1:4，而单价比为3:2:1，如果丙种糖果买了72袋，那么甲乙两种糖果一共是( )袋。

「答案解析」

设甲的单价为3，乙的单价为2，丙的单价为1，则丙的总价为72，

根据总价比，那么乙的总价就是：

甲的总价就是：

因此，乙买了：

甲买了：

甲乙两种糖果一共买了袋。

14、某次数学竞赛设一、二、三等奖，已知:

①甲、乙两校获一等奖人数比为1:2，且两校获奖总人数之比是5:4；

②甲、乙两校获二等奖人数占两校获奖人数总和的 ，其中乙校是甲校的3.5倍；

③甲校三等奖获奖人数占该校获奖人数的 。

请问：乙校获三等奖人数占该校获奖人数的(    )%。

「答案解析」

看起来很绕，我们就直接假设甲校获奖人数为份，则乙校获奖人数为份。

根据条件②，那甲乙两校或二等奖人数就是：

由于乙校的二等奖人数是甲校的3.5倍，那么乙校的二等奖人数为：

那甲校的二等奖人数就是：

根据条件③，那甲校三等奖获奖人数就是：

因此，甲校一等奖人数就是：

根据条件①，那乙校的一等奖人数就是：

那乙校三等奖获奖人数就是：

占比就是：

15、一个水池有甲、乙、丙三个水管，甲乙是进水管，丙是排水管。单开甲管20分钟可以将水池注满，单开乙管20分钟可以将水池注满，单开丙管25分钟可以将水池的水放完，现在先开甲乙两管，4分钟后关上甲管开丙管，问：又经过(     )分钟才能将水池注满。

「答案解析」

单开甲管或乙管注水的效率是 ，单开丙管排水的效率是 。

先开甲乙两管4分钟，则注水占的比重是：

以后关上甲管打开丙管，则注水效率是：

因此，还需要花的时间就是：

16、有一个圆柱和一个圆锥，圆柱的底面直径和高都是8，圆锥的底面和高都是4，单位是厘米。圆柱体积是圆锥体积的(    )倍。

「答案解析」

底面直径是2倍，高也是2倍，

那么圆柱的体积是圆锥的：

倍。

17、一个透明的封闭盛水容器，由一个圆柱体和一个圆锥体组成，圆柱体的底面直径和高都是10厘米。其内有一些水，正放时水面离容器顶9厘米，倒放时水面离顶部5厘米，那么这个容器的容积是(     )立方厘米。

「答案解析」

这种题目我们可以画一画示意图：

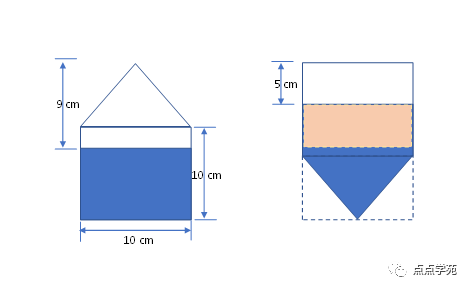
可以看到，倒立后，下方2倍圆锥体体积的水都跑上去了，导致空白部分的高度从9厘米缩短到了5厘米。

因此，倒立后圆柱体内的水高了厘米，也就是上图右边黄色部分表示的体积。

比较上图的左右两个部分的下半段，

在左图中，和圆锥体登高的圆柱部分是圆锥体的3倍，其中有的部分转移到上面所说的黄色部分去了。

因此，转移的这部分水的体积其实也等于圆锥体体积的两倍，因此，圆锥体的高就是：

因此，容器的体积就是：

18、有一个圆柱体，高是底面半径的4倍，从中间截断将它分成大、小两个圆柱体，如果大圆柱体的表面积是小圆柱体的表面积的3倍，那么大圆柱体的体积是小圆柱体的体积的()倍。

「答案解析」

大圆柱体和小圆柱体的底面积相同，

设底面半径为1，则原来的圆柱的高是4，设截断后大圆柱体的高是h，则小圆柱体的高是4-h，

有

消去两边的共同项，也就是：

解得：

因此，大圆柱的体积就是小圆柱体的：

倍。

19、某水库建有10个泄洪闸，现有水库的水位已经超过安全线，上游河水还在按不变的速度流入。为了防洪，需调节泄洪速度。假设每个闸门泄洪速度相同，经测算，若打开一个泄洪闸，30小时水位降至安全线；若打开2个泄洪闸，10个小时水位降至安全线。现在抗洪指挥部要求在3小时使水位降至安全线以下，至少要同时打开(    )个闸门。

「答案解析」

我们将该水库看作一个水箱，上游来水看作进水管，泄洪闸看作出水管，安全水位就相当于将水箱排空。

因此，上游进水由原来的个小时降至个小时，流入量减少的数量为：

相当于减少了进水速度的20倍。

泄洪由原来的1个闸工作30个小时降至2个闸工作10小时，减少的水量为：

出水量相当于减少了泄洪速度的10倍。

由于两者减少的水量总体是相等的，因此，出水的速度就是进水的速度

倍。

所以，进水30个小时就可将该水库灌满。

如果要求3小时将水位降至安全线以下，需要排空的水量就是：

倍的进水时间。

需要的泄洪闸数量就是：

相当于至少要开6个泄洪闸。

如果想不明白，我们可以设方程，假设进水速度是，出水速度是，超过安全水位线的水的容量是，

则有如下方程：

两式相减，消去，可得：

因此，。

假设需要个泄洪闸，那么就有如下关系：

也就是：

所以，，因此，向上取整，就相当于要同时开6个泄洪闸。

20、如图，有一个敞口的立方体水箱，在其侧面一条高的三等分点处有两个排水孔A和B，它们排水时的速度相同且保持不变。现在以一定的速度从上面往水箱注水，如果打开A孔、关闭B孔，经过30分钟可将水箱注满；如果关闭A孔，打开B孔，经过33分钟可将水箱注满，如果两个孔都打开，那么注满水箱的时间是(    )分钟。

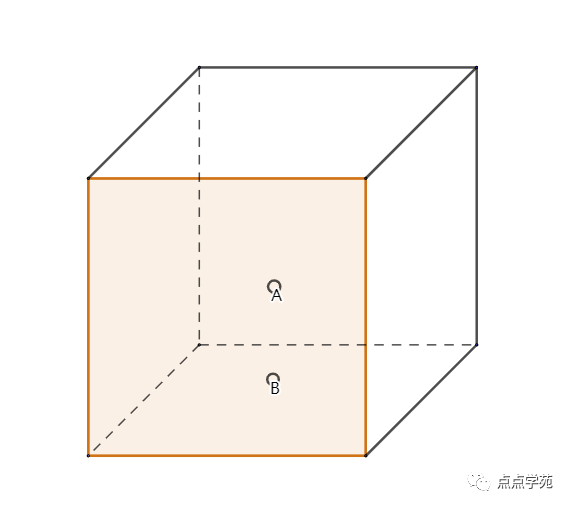
「答案解析」

我们要弄明白，为什么只开A孔和只开B孔的时间会差了3分钟。

如上图所示，水箱的体积可以分成三等分。

假设注水速度为a，单孔排水速度为b。

（1）注满水箱前。

这个时候，只有注入没有流出，只开A孔和只开B孔的速度是一样的，这两种方式不会产生时间差异。

（2）注满水箱后。

这个时候，既有注入又有流出，只A孔和只开B孔的速度也是一样的，这个时候也不会产生时间差异。

（3）注满水箱中间的。

只开A孔的时候只有流入，没有流出。只开B孔的时候，既有流入也有流出。这个时候，注水时间就会存在差异。

那这也说明，只注入不流出（速度为a)这种情况要比既注入又流出（速度为a-b）这种情况节省：

同理，只有流入，没有流出，一直保持流入a的速度，那注满水箱需要的时间就是：

同样，既有流入又有流出，一直保持速度为a-b的情况，那注满水箱需要的时间就是：

因此，只流入的效率就是，既流入又流出的效率就是，

那么，流出的效率就是：

也就是，在水箱注满水的情况下，只排水，则需要耗时108分钟。

因此，如果将A孔和B孔移动到水箱底部，同时注水和排水，需要的时间就是：

因此，按题意，既注水，又打开A孔和B孔，则需要的时间就是：

这道题目如果想不明白，用方程解答就快速些。

设进水速度为，每个口的出水速度为，水箱的体积为1，则：

这属于二元一次方程组，看起来很复杂，仔细观察后，我们可以将看作一个整体，也可以用换元法来简化。

也可以通过消去，有：

代回原式，可以解得，

因此，。

那么将两个孔都打开，灌满水箱的时间就是：

也就是：

微信公众号搜索： 北京小学学习资料     家长升学指南  关注公众号，获取最新资讯！

扫码添加“家长论坛”微信好友（微信号 16619908263）

获取YMO世界青少年奥林匹克数学竞赛选拔赛决赛试卷真题
咨询YMO世界青少年奥林匹克数学竞赛政策请拨打电话 16619908263 （同微信号）