[数学]第27届YMO交流活动小学6年级初赛试题

点击领取>>>YMO世界青少年奥林匹克数学竞赛选拔赛决赛试卷题

1.1、(   )

「答案解析」

注意观察，要利用下式子里的20。

1.2、(   )

「答案解析」

提取公因式。

1.3、(   )

「答案解析」

注意利用平方差公式：

所以：

利用首尾相加法：

1.4、(    )

「答案解析」

此题不能使用裂项求和法，参考前面发布的第28届试题，题目相同。

[数学]第28届YMO交流活动6年级初赛试题

这里要利用下面的公式：

注意到分母里的每项里的两个乘数之和都是301，因此，我们可以提取一个301出来，

所以：

后面那段大分数项等于1，所以。

2、计算：

那么，(    )。

「答案解析」

这个只能死算，交叉相乘，可以解得：

同样，可以解得：

3、商店一次进货6桐油，质量（单位为千克）分别为15，16、18、19、20、 31，上午卖出去2桶，下午卖出去3桶，下午卖出去的油刚好是上午卖出去的2倍，下午卖出去的油共重(    )千克。

「答案解析」

仔细分析题意，为了方便描述，不妨设下午卖出去的油是，上午卖出去的油是，

那么，必有：

因此，下午卖出去的油的质量一定是个偶数。

同时，有：

因此，卖出去的油一定是3的倍数。

而，

因此，没有卖出去的油只能是20千克。

而：

因此，

因此，下午卖出去的油就是千克。

可以验算下，看看是哪三桶油一共重66千克。

4、如下图，在直角三角形ABC中，D是斜边AB上一点，正方形CEDF的边长是7，若灰色部分（棋盘）的积是35，则中间阴影(斜线)部分的面积是(    )。

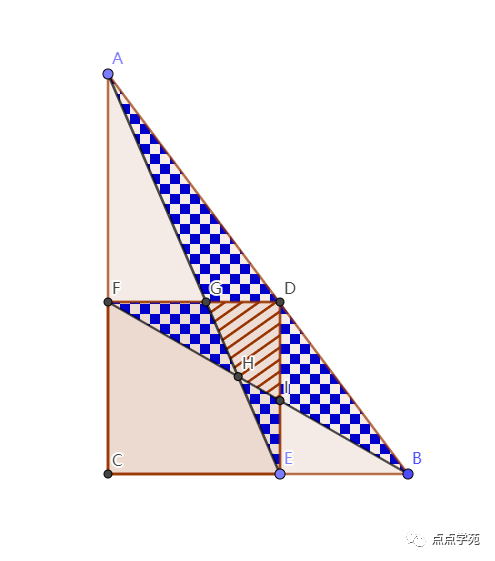
「答案解析」

小学的几何一般就是用一半模型、蝴蝶模型，或者面积比例等几个比较简单的方法，还有旋转、对称之类的方法。

这个题目想复杂了的话，如果用平面几何，或者面积比例关系的话，计算量非常大。

其实，我们可以用一半模型来解决它。

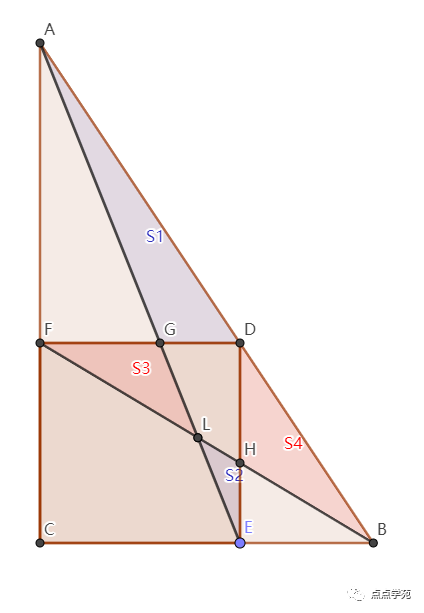
如上图所示，我们记所求的四边形面积为s，记其他四个三角形的面积分别为s1、S2、S3、S4。

仔细观察，根据等底等高的三角形和矩形的面积关系，我们可以发现：

由于：

所以：

其中，，所以：

也就是说，所求四边形的面积为7。

5、从101到900的自然数中，数字和能被8整除的数共有(   )个。

「答案解析」

这道题，在第28届YMO六年级初赛中出现过，请参考前面发表的解析。

[数学]第28届YMO交流活动6年级初赛试题

考虑一个三位数的十位和个位，十位数上可以选择0到9，个位上也可以选择0到9，那么后两位就有种选择方法。只要后两位固定了，那么百位数上总能从1到8中挑一个出来，从而使得数字和被8整除。

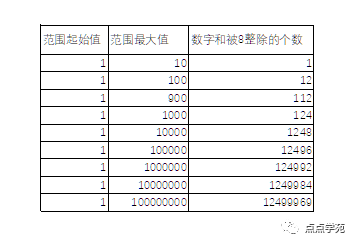
可以看到，数字和类的题目也只能针对三位数出题了。

6、是(   )的平方。

「答案解析」

看着很吓人，前面的这样的阶梯数是5个1，也就是的倍数。阶梯数里最高数字是几，就是几位全1数的倍数。

所以是的平方。

7、已知九位数既是9的倍数，又是11的倍数，那么，这个九位数是(    )。

「答案解析」

根据整除的特征，有：

同时，有：

因为A和B都是小于9的数字，所以，有：

所以，

所以，这个九位数是。

8、把102分拆成三个不同质数的和，共有(   )种方法。

「答案解析」

除了2以外，其他的质数都是奇数，而102是偶数，所以三个数中必定有2。

那么，其他两个质数的和是100。

在脑袋里遍历下质数表，可以搜寻到：

所以，一共有6种方法。

9、四个人传球，每个人不能传给自己，如果初始时球在A手中，经过4次传球后仍然回到A手中，那么共有(   )种不同的传球方式。

「答案解析」

参考第28届YMO六年级初赛第15题。

[数学]第28届YMO交流活动6年级初赛试题

本题是4个人，第15题是4个城市。差别只在于本题只有4次传球，第15题是经过了5个城市。

因此，本题共有种方式。

10、一个自然数分别与另外两个相邻奇数相乘，所得的两个积相差190，那么这个数是(    )。

「答案解析」

相邻奇数差2，因此这个数是。

41、一个偶数的数字和是41，这个偶数最小是(    )。

「答案解析」

要想偶数最小，末位一定是8，中间位尽量是9。

因此，首位是6，末位是8，中间3位是9。

这个偶数就是。

12、甲、乙、丙三人进行万米赛跑，甲是最后一个起跑的，在整个比赛过程中，甲与乙、丙的位置共交换了7次，则比赛的结果甲是第(    )名。

「答案解析」

参考第28届YMO六年级初赛第18题。

[数学]第28届YMO交流活动6年级初赛试题

交换了1次，甲肯定就是第二名。

再交换1次，甲不是第一名就是第三名，再交换1次，甲又回到了第二名。

可以看到，只要是交换了奇数次，甲就会回到第二名。

13、有些数，它的各位数字之积是质数，我们称这样的自然数是“YMO数”，小于10000的最大“YMO数”是(    )。

「答案解析」

参考第28届YMO六年级初赛第12题。

[数学]第28届YMO交流活动6年级初赛试题

一位数字，最大的质数是7，最小的是2。

既然各位数字之积是质数，那么只能是某个质数和多个1相乘。

因此，小于10000的最大YMO数就是。

14、将55拆成10个质数之和，要求最大的质数尽可能小，那么其中最大的质数是(    ）。

「答案解析」

除了质数2，其余的质数都是奇数，因此，偶数个非2质数之和必定是偶数。

因此，其中必有一个质数2。

那么，其他9个质数的平均值为，平均值在5和6之间。

猜测最大的质数就是7，那么比7小的其他质数就只有3和5了。

假设3有x个，5有y个，7有z个，有如下不定方程组：

用，可以得到：

我们可以尝试下让，则，那么，经验证，满足要求。

很明显，，那么，就说明最小的质数就是7。

15、，那么(    )。

「答案解析」

从等式可以推论出：

从而可以推出：

16、六位数能被44整除，那么这个六位数最大为(    )。

「答案解析」

该数能被4和11整除，那么2B能被4整除，那么B就可以是0、 4或8。

那么：

所以，或5，

所以，存在下面几组解：

所以，该六位数就是。

17、的结果为，那么=(   )。

「答案解析」

所以，。

所以，根据被11整除的特征，有：

也就是：

所以，。

所以，。

18、有一楼梯共有12级，每步可以走1级或者2级，要求第6级必须要踩到，12级全部走完共有(      )种不同的走法。

「答案解析」

这道题容易想道的就是分类汇总，前面的6级楼梯，可以按如下方式分类：

(1)每步走1级：只有1种走法。

(2)四步走1级，一步走2级：只有5种走法。

(3)两步走1级，两步走2级：只有6种走法。

(4)每步走2级：只有1种走法。

所以，前面6级楼梯有种走法。

同理，后面6级楼梯也有13种走法。

因此，一共有种走法。

但如果中间的第6步没有必须要求踩到，再用上面的分类汇总就非常麻烦，类别太多，每个类也不好统计。

这种题目其实有一种更巧妙的办法，其实就是递归。

假设有N级，我们第一步走1级，那剩下就有N-1级楼梯要走，那在N-1级楼梯里，是不是又碰到了一模一样要解决的问题呢？这种方法就叫递归。

同时，如果我们第二步走2级，那剩下就有N-2级楼梯要走，在这N-2级楼梯里，又碰到了一样的问题。

在编程中，我们将此种方法定义为一个函数F，那么N级楼梯的走法就是F(N)种，那么N-1级楼梯的走法就是F(N-1)种，那N-2级就是F(N-2)种。

既然允许走1步或2步，那么，，这里的，。

这就是那个有名的斐波拉契数列问题。

19、有一口井，每小时涌出的水量相同。用甲抽水机抽水，20小时可以抽干；用乙抽水机抽水，30小时可以抽干；若甲乙同时抽水，8小时可以抽干。那么这口井抽干之后，(    )小时又可涌满。

「答案解析」

用甲抽水的时候，抽水减去进水的效率差是，用乙抽水的时候，抽水减去进水的的效率是。

因此，这两个数值相加的时候，恰好多了一次进水的效率。

因此，进水的效率就是：

也就是，24小数后，空井就会被灌满。

20、有一项工程，甲单独做需要36天完成，乙单独做需要30天完成，丙单独做需要48天完成，现在由甲、乙、丙三人同时做，在工作期间，丙休息了整数天，而甲和乙一直工作至完成，最后完成这项工程也用了整数天，那么丙休息了(    )天。

「答案解析」

甲乙丙的效率之和为：

甲乙的效率之和为：

设甲乙丙一起工作了天，丙休息后，甲乙一起工作了天，有：

也就是：

从而可得：

可以令，继续缩小范围。也可以通过观察法来确认的值。

也可以将后面的分数转换成如下方程：

很明显，是符合要求的唯一解。

那么，，也就是丙休息了11天。

微信公众号搜索： 北京小学学习资料     家长升学指南  关注公众号，获取最新资讯！

扫码添加“家长论坛”微信好友（微信号 16619908263）

获取YMO世界青少年奥林匹克数学竞赛选拔赛决赛试卷真题
咨询YMO世界青少年奥林匹克数学竞赛政策请拨打电话 16619908263 （同微信号）