[数学]第26届YMO交流活动小学6年级初赛试题

点击领取>>>YMO世界青少年奥林匹克数学竞赛选拔赛决赛试卷题

1、甲、乙二人各走一段路，他们速度比是，时间比是，则路程比是(   )

A、

B、

C、

D、

「答案解析」

路程等于速度乘上时间，

假设甲的速度是3，时间是8；乙的速度是5，速度是9，则路程比是：

直接假设，容易理解。选D。

2、甲乙两个非零自然数，如果甲数的恰好是乙数的，那么甲乙两数之和的最小值是(   )

A、13

B、24

C、15

D、31

「答案解析」

依据题意，甲数的再乘上，也是乙数的的，

因此，甲等于乙的，如果乙是16，那么甲就是15，选D。

3.一个六位数，它的个位上的数字是9，如果把数字9移到第一位得到的新数是原数的4倍。原来的六位数是(   )。

A、320679

B、230769

C、345789

D、245169

「答案解析」

设前面五位数是，有：

也就是：

解得，选B。

4，用一幅学生用的三角板的内角，可以画出大于0°且小于176°的不同角度的角共有（   ）种。

A、8

B、9

C、10

D、11

「答案解析」

三角板有30°、45°、60°、90°等几种角度，基本上可以画出的n倍角，那平角相当于12个15°角。

选D。

5、师徒两人加工一批零件，师傅加工一个零件用9分钟，徒弟加工一个零件用15分钟，完成任务时，师傅比徒弟多加工100个零件，求师傅和徒弟一共加工零件。

A、280

B、360

C、400

D、450

「答案解析」

基本的工程问题。

师徒两人用时：

一共加工的零件就是：

选C。

6、一本书，已读页数与未读页数之比是，如果再读页，已读页数与剩下页数之比是。这本书共有( )页。

A、429

B、924

C、249

D、294

「答案解析」

选B。

7、完成一项工作，甲、乙两人合作需15小时，乙、丙两人合作需12小时，甲、丙合作需 10 小时。甲、乙、丙三人合作需(     )小时完成。

A、6

B、7

C、8

D、9

「答案解析」

甲乙丙的效率就是：

因此，选C。

8、数的末两位数字是(    )。

4、16

B、36

C、76

D、96

「答案解析」

对小学生来说，可以老老实实地通过找规律的方法来确认末两位数。

可以看到，从2次幂开始，每5次一循环。而：

因此，末两位和5位一循环里的第三顺位96相同。

因此，的末两位数就是96。

选D。

本来此类方法用欧拉定理来解答更直接些，但由于和不互质，难度就稍微大一点。

参考：【数学 | 初等数论】[03]欧拉定理学习笔记

9、如图所示，长方形ABCD的面积为24平方厘米，三角形ABE、AFD的面积均为4平方厘米，求三 角形AEF的面积是（     )平方厘米。

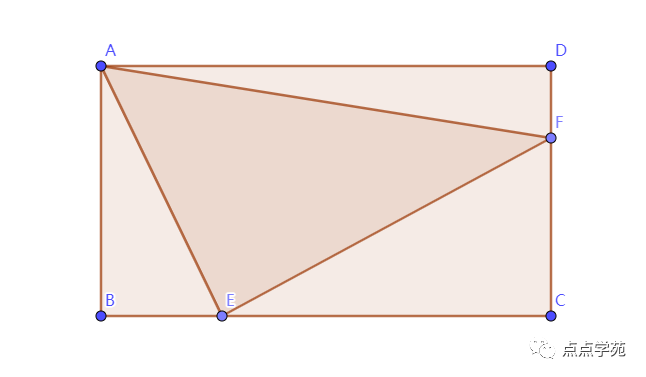
A、

B、

C、10

D、11

「答案解析」

如图所示，做两条辅助线。

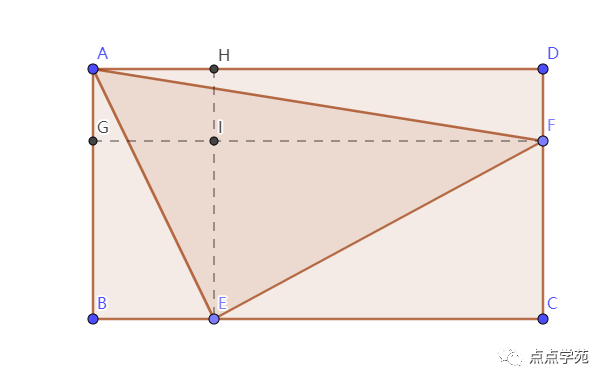
在长方形ABCD中，三角形ADF和三角形ABE的面积占比都为，那就说明：

说明三角形CEF的面积就是：

因此，三角形AEF的面积就是：

选B。

10、x、y、z是三个非零自然数，且，那么三数按从大到小的顺序排列应该是（   ）。A

A、x>y>z

B、z>y>x

C、y>x>z

D、y>z>x

「答案解析」

此题简单，选B。

1、A、B分解质因数后分别是：，，A、B的最大公因数是(    ），最小公倍数是(    )。

「答案解析」

最小公倍数就是，最大公因数就是。

2、一位水果商以1.8元/千克的进价购入5000千克的橘子。假设批橘子的运费为3000元，在运输途中损坏了10%的橘子，最后所有未损坏的橘子全部被售出，并且这位水果商获得5%的盈利那么这位水果商是将橘子以每千克(      )元售出。

「答案解析」

成本是元，实际销售的橘子的质量是千克。

加上利润，销售的总价必须为元。

因此，售价将以每千克元卖出。

3、养鱼塘里养了一批家鱼，第一次捕上来100尾，涂上不褪色的红色标记后放回鱼塘。数月后又捕上100尾，发现涂有红色记号的为5尾，则鱼塘里原来大约有(       )尾。

「答案解析」

捕上来的标有记号的鱼占比为，那我们只能假设标有红色记号的鱼在池塘里的占比也是5%了。

因此，鱼塘里的鱼有尾。

4、春节联欢晚会时，2020盏彩灯(各由一个拉线开关控制)大放光明。小真把编号是6的倍数的开关各拉一次，小聪把编号是19的倍数的开关各拉一次，小明把编号是29的倍数的开关各拉一次。这时有(    )盏彩灯是亮的。

「答案解析」

仔细分析，既然彩灯大放光明，只能假设彩灯开始都是亮着的。

由于，说明这里面的灯没有被拉过三次，很明显，拉过一次的灯都关了，拉过两次的灯又开了。

拉过一次或两次的灯的数量是：

拉过两次的灯的数量是：

那么，没有被拉过灯加上拉过两次的灯就是：

也就是说，最后亮着的灯有盏。

5、将一堆苹果全部分给甲、乙、丙三个小朋友。原计划甲、乙、丙三人所得苹果个数的比为。实际上，甲、乙、丙三人所得苹果数的比为，其中有一位小朋友比原计划多得了5个苹果。那么这位小朋友是(    )(填“甲”、“乙”或“丙”)，他实际所得的苹果数为(    )个。

「答案解析」

甲分到的苹果的占比变化是：

乙是：

丙是：

因此，这个小朋友是丙。

实际所得的苹果是：

个。

6、有一个水池，第一次放出全部水的，第二次放出 30立方米水，第三次又放出剩下水的，池里还剩水54立方米，全池蓄水为  (    )立方米。

「答案解析」

倒推法来解题。

立方米。

7、甲、乙两车同时从A城出发，开往相距750千米的B城，甲车每小时行68千米，乙车每小时行57千米，甲车到达B城后立刻返回。两车从出发到相遇一共经过(      )小时。

「答案解析」

甲车到达B城时，耗时是：

此时甲车返回，就变成了相遇问题，所花时间就是：

因此，两车从出发到相遇一共耗时：

8、某仓库的门上有若干把锁，且有11位管理人员身上分别带有若干把钥匙，其中任何5人都不能 把锁全部打开，而任何6人都可以全部把锁打开，那么这个仓库的门上至少有(    )把锁。

「答案解析」

这是一道排列组合题，难以理解，这仓库的门得有多大呢？

任意5人不能把锁打开，说明这5把钥匙少了，而这样的任意5人一共有种可能，说明这任意5人可以持有462把不同的钥匙。

因此，至少有462把锁，只要再来一个人，就可以将全部锁打开。

9、一个大正方体由个一样的小正方体堆成，如果将其表面涂成红色，那么其中一面被涂成红色有(    )块，面涂色的小正方体有(    )块，三面涂色的小正方体有(    )块，每个面都不涂色的小正方体有(     )块。

「答案解析」

玩过魔方的容易理解。

一面涂有红色的有：

两面涂有红色的有：

三面涂有红色的就是顶点，有8块。

每个面都不涂色的就有：

10、在一场绕着环形车道的汽车比赛中，其中一辆28号车的前面汽车数量的加上这辆汽车后面汽 车数量的恰好就是本次汽车比赛的赛车总数，那么这场比赛共有(      )辆汽车。

「答案解析」

设共有x辆汽车。

解得。

11、一项工程，由甲队单独工作需要15天完成，由乙队单独工作需要12天完成，由丙队单独工作 需要10天完成。现在由甲、乙两个工程队共同工作了3天后，剩下的工程由丙队单独完成，丙队还需要(      )天才能完成项工程。

「答案解析」

简单的工程问题。

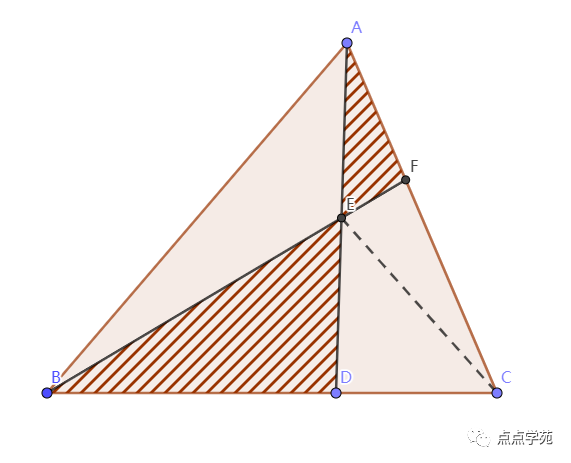
12、如图，三角形ABC的面积为60平方分米，，，求阴影部分的面积是(    )平方分米。

「答案解析」

连接。

由于，所以

平方分米，

平方分米，

平方分米。

由于，所以

平方分米，

平方分米。

根据比例关系，有：

所以：

平方分米。

所以，阴影部分的面积就是平方分米。

13、一个口袋中有100个球，其中红球有28个，绿球有20个，黄球有12个，蓝球有20个，白球有10个，黑球有10个，从口袋中任意摸出球来，如果要使模出的球中，至少有12个颜色相同，那么从口袋中至少要模出(     )个球来。

「答案解析」

运气不好的话，我们摸完10轮，可以确保每种颜色各有一个，此时共摸出个球。

刚好白球和黑球已经模完。

再摸1轮，此时红绿黄蓝各有11个，继续再摸一个，就可确保有12个球同色。

因此，摸出的总球数就是个。

14、角、、中有两个锐角和一个钝角，其数值已经给出，在计算时，甲乙丙丁四人得到、、、这样四个不同的结果，其中只有一个结果是正确的，那么的值是（     ）。

「答案解析」

角、、中有两个锐角和一个钝角，这句话透露出来的是什么意思呢？

意思就是三角之和有个范围，必定大于，小于。

根据乙的计算结果，我们反推出三角之和，根据条件，这是不可能的。

因此，只有甲是计算正确的，三角之和为。

15、在一个棱长为5分米的正方体上放一个棱长为4分米的小正方体，这个立方图形的表面积是（   ）平方分米。

「答案解析」

按题目的意思，这个立方图形的表面积刚好是大立方体的表面积加上小立方体的侧面积。

完毕。

微信公众号搜索： 北京小学学习资料     家长升学指南  关注公众号，获取最新资讯！

扫码添加“家长论坛”微信好友（微信号 16619908263）

获取YMO世界青少年奥林匹克数学竞赛选拔赛决赛试卷真题
咨询YMO世界青少年奥林匹克数学竞赛政策请拨打电话 16619908263 （同微信号）