[数学]第25届YMO交流活动小学6年级初赛试题

点击领取>>>YMO世界青少年奥林匹克数学竞赛选拔赛决赛试卷题

1、下列选项中，不可能围成封闭的正方体的是（    ）。

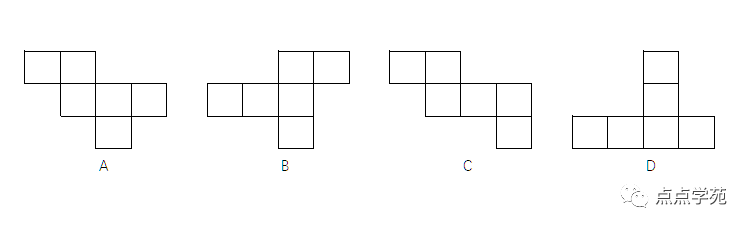
「答案解析」

这个考的就是空间想象力了，前面三个都没看，就挑了最明显的D看了看，发现是不可能的，围起来的时候图里最上面那个面就重叠了。

选D。

2、用剪刀将40厘米长的细绳子剪成长度分别为10厘米，20厘米和10厘米的三段，细绳可以弯折，最少要剪（     ）次。

A、1

B、2

C、3

D、4

「答案解析」

将绳子对折，然后挑中点剪一刀，就可达到目的。

因此，选A。

3、如图，一个三角形的三个顶点分别为三个半径为4厘米的圆的圆心，则图中阴影部分的面积是（    ）平方厘米。

A、

B、

C、

D、

❞

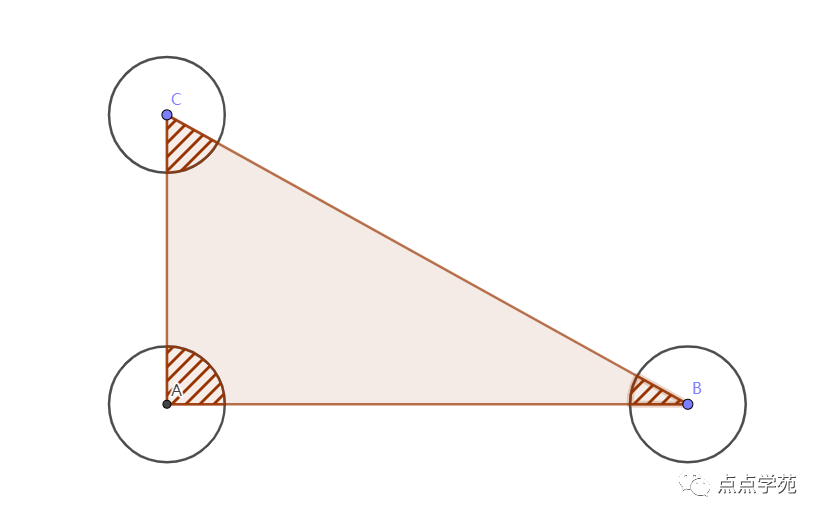
「答案解析」

三角形内角和为，因此，阴影部分就是一个半圆，面积就是。

选B。

4、2020的所有因数里，是5的倍数的合计有（    ）个。

A、12

B、10

C、7

D、6

「答案解析」

因为，除了5以外，2可以选3次，101可以选2次。

所以5的倍数合计有：

选D。

5、甲乙两人各走一段路，他们的速度之比是3:4，路程比是8:3，那么他们所需要的时间比是（    ）。

A、2:1

B、32:9

C、1:2

D、4:3

「答案解析」

根据公式，可以算出时间之比就是：

选B。

6、把一个圆柱分成相等的四个圆柱，表面积增加18.84平方分米，则圆柱的一个底面的面积是(   )平方分米。

A、3.14

B、4.71

C、6.28

D、9.42

「答案解析」

按题意，底面积增加了倍，因此，底面积为：

选A。

7、在比例尺是1:3000000的地图上，量得A、B两港距离为12厘米，一艘货轮于上午7时以每小时24千米的速度从A开向B港，到达B港的时间是（     ）点。

A、22

B、20

C、18

D、16

「答案解析」

关键是要理解地图上的比例尺代表的意思。

在1:3000000的地图上，代表的是地图上的1厘米代表实际中的3000000厘米，转换成千米就是30千米。

因此，到达B港的耗时就是：

晚上到达的时间就是：。

选A。

8、师傅和徒弟加工一批零件，师傅加工这批零件需要9小时，徒弟加工这批零件需要15小时，那么徒弟比师傅（   ）。

A、快60%

B、慢60%

C、快40%

D、慢40%

「答案解析」

师傅的效率比徒弟要高，排除A和C。

选D。

9、分母为100的最简分数有（    ）个。

A、40

B、50

C、60

D、无数

「答案解析」

最简分数和最简真分数都是些什么意思呢？我们要明白这是什么概念。

如果求最简真分数，那我们就是要排除掉100以内2和5的倍数，学过欧拉定理的就知道有个欧拉函数。

没有公因数的数有：

如果不清楚，我们就死算。

100以内2的倍数有50个，5的倍数有20个，10的倍数有10个。

我们算2和5的倍数的时候，10的倍数被重复计算了。

因此，和100有公因数2和5的数就有个，没有公因数的就是40个。

这个道理和欧拉函数是一样的。

所以，如果是求最简真分数，此道题就选A。

但由于最简分数可以大于1，因此，答案就可以无数。

选D。

10、200个5连乘的积，是一个(   )位数。

A、120

B、139

C、140

D、141

「答案解析」

为了方便表述，我们假设其是一个位数，用科学计数法来表示，那么就有：

上面的a是一个小于10的正数。

因此，也就是求：

我们不考虑a，大概就是要找出这样的x，使：

如果我们手头有计算器，或者学过对数，大概可以估算出或查到。

那么我们就可列出如下方程：

解得。

那么，就选C。

但从小学生的思维来考虑，编者也暂时想不出什么好办法。

只能注意到，也就是说。

那么，也会有，也就是，

从而。

是一个141位数，由于，，那么，因此，我们猜测是一个140位数。

严谨一点的话，我们需要确认下，这对小学生来说有点难，这里我们就不确认了。

1、一台综艺节目，由2个不同的舞蹈和4个不同的演唱组成。如果第一个节目是舞蹈，第二个节目是演唱，接下来的节目没有限制，那么共有（    ）种不同的安排方法。

「答案解析」

排列组合题。

第一个节目有两种选法，第二个节目有四种选法，后面四个节目就是从4个里面挑4个。

完毕。

2、有浓度为20%的糖水200克，另有浓度为48%的糖水150克，将它们混合摇匀后的浓度为(   )%。

「答案解析」

此题简单，根据关系可列出算式：

也就是：

所以，浓度为32%。

3、从1到2020的所有自然数中，乘128后是完全平方数的数共有（   ）个。

「答案解析」

由于，所以，满足要求的数可以写成：

所以，，也就是

所以，最大可以是31。

所以，这样的数一共有31个。

4、小Y、小M和小O都从甲地到乙地，按原定速度小Y比小M早到9分钟，三人同时从甲地出发，10分钟后遇到下雨道路泥泞，小Y速度下降了40%，小M速度下降了25%，小O速度下降35%，结果三人同时到达乙地，那么小O原定行驶完全程需要（     ）分钟。

「答案解析」

假设小Y的原定耗时是y，小M的原定耗时是m，小O的原定耗时是o。

由于小Y比小M快9分钟，因此有：。

小Y在剩下的路程里，如果降速行驶，那么耗时将会变成。

同理，小M的耗时会变成，小O的耗时就会变成。

由于降速后的耗时相等，那么有：

由于

因此，有：

可以解得分钟，分钟。

从而，有：

可以解得分钟，

也就是说，小O行驶完全程需要49分钟。

5、把1、2、3、4、5这5个数字各使用一次排成五位数，所能排出的五位数按从小到大的顺序排列，那么排在最中间的两个五位数的和是（    ）。

「答案解析」

这个不要被吓唬住了。

最小的数是12345，最大的数是54321，其和是66666。

第二小的数是12354，第二大的数是54312，其和也是66666。

这五个数无论怎么排列，能排列出的总数肯定是个偶数。

因此，按着类似规律排列，最中间的两个的和也是66666。

6、用1、2、3、4、5、6各一次且必须全部用到，组成几个质数，这些质数之和最小为（     ）。

「答案解析」

此道题以前理解有误，不是组成一个6位数的质数，而是用这些数字组成若干个质数。

由于2、4、5、6不适合放在末位，那放在末位的只能是3和1。

要想和最小，那这些质数最大的最好是两位数。

那么，我们就可以拼出来的质数只能是:

因此，质数之和最小为111。

7、如图所示，正方形的边长为3厘米，BG=AE=CH=DF=1，空白部分的面积为（    ）平方厘米。

❞

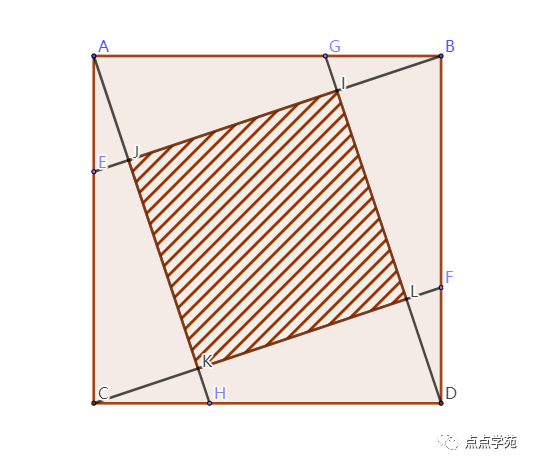
「答案解析」

根据比例关系，有：

所以：

而，

所以：

所以，平方厘米。

所以，平方厘米。

因此，空白部分的面积就是：

完毕。

8、如图所示，长方形ABCD中，E、F、G、H分别是各边中点。已知大长方形的面积是128平方厘米，则阴影部分的面积是(    )平方厘米。

❞

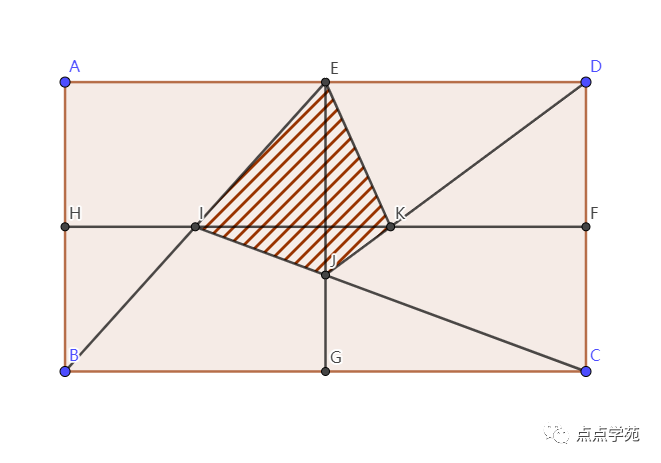
「答案解析」

根据等底同高的三角形面积是矩形面积的一半，也就是小学里常说的一半原理。

那么，平方厘米。

而

因此，阴影部分的面积就是平方厘米。

9、如果，正方形ABCD的面积是200平方厘米，那么阴影圆环的面积是（   ）平方厘米。

❞

「答案解析」

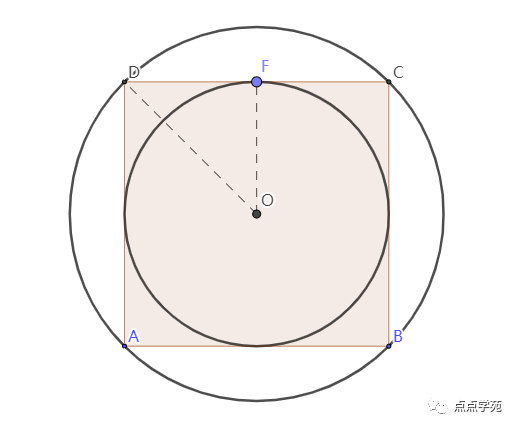
设圆环的外径为，内径为，则圆环的面积为：

如果知道勾股定理，就可以知道。

或者根据面积关系，

可以知道，

从而，圆环的面积就是：。

10、自然数2019的数字之和是，则1至2019所有自然数的全部数字之和是（     ）。

「答案解析」

从0至9，数字和是。

再考虑两位数，从0至99，可以看到，个位数上有10个0至9，十位数上也有10个0至9，所有数字之和就是。

上面的关系想清楚后，我们开始考虑从0到999的三位数。

可以看到，个位数上有100个0至9，那数字之和就是。十位数和百位数一样，那总共的数字就有。

再考虑从1000至1999的四位数。

跟前面的三位数相比，至少千位数上多了1000个1，因此，该范围之内的数字之和就是。

再考虑从2000至2019这20个数字，数字之和就是。

因此，所求的数字之和就是。

11、甲、乙地相距3840米，其中一部分是上坡路，其余是下坡路，某人骑自行车从甲地到乙地后沿原路返回。去时用了2小时48分，返回时用了2小时32分。已知自行车上坡速度是每小时12千米，那么自行车下坡的速度是（    ）千米/时。

「答案解析」

一来一回，说明上坡和下坡各走了一个全程。

这道题目感觉出错了，按上坡每小时12千米的速度，全程上坡的耗时只要：

而一来一回总共耗时是5小时20分，也就是小时。

由于上坡较慢，下坡快，那么上坡的耗时肯定大于小时，因此，本题出错了。

甲乙两地相距可能是38400米而不是3840米，这样，上坡全程就用了小时，也就是小时。

因此，全程下坡用的时间就是小时。

所以，下坡的速度就是：

完毕。

12、甲、乙分别从A，B两地同时相向出发。相遇时，甲、乙两人速度比是4∶5。从相遇算起，甲到达B地与乙到达A地所用的时间比是（    ）。

「答案解析」

假设甲乙两人都是匀速行驶的，速度比一直是4:5，那两人相遇后待行驶的路程比就是。

因此，相遇后两人耗时相比为：

完毕。

13、已知，则(____)

「答案解析」

根据已知条件，先通分，有，然后将其作为一个整体代入：

完毕。

14、称能表示成的形式的自然数为三角数，有一个四位数N，它既是三角数，又是完全平方数，则（____）。

「答案解析」

首位相加可以得知三角数，那么有：

由于k和k+1是连续的两个整数，那么可以算得：

主要依据就是，。

由于连续的两个数互质，那要么是个平方数，要么是个平方数。

（1）我们先考虑是个平方数，那么也是个平方数，并且只能是奇数。

那么，符合条件的只能有：

如果，很巧，也是一个平方数，那么。

这里刚好碰巧找到了一个合适的解，那这个解在四位数中是唯一的吗？

我们依次验证，可以发现和不符合要求。

（2）那我们再考虑是个平方数，那么也是个平方数。

那么，符合条件的  只能有：

依次验证，发现，，，时，都不是完全平方数。

综上所述，满足条件的四位数。

15、甲、乙两人分别从A、B两地同时出发相向而行，6小时后相遇在C点。如果甲速度不变，乙每小时多行3千米，且甲、乙还从A、B两地同时出发相向而行，则相遇点D距C点9千米;如果乙速度不变，甲每小时多行4千米，且甲乙还从A、B两地同时出发相向而行，则相遇点E距C点8千米。则甲原来的速度是(____)千米/时。

「答案解析」

示意图如下所示：

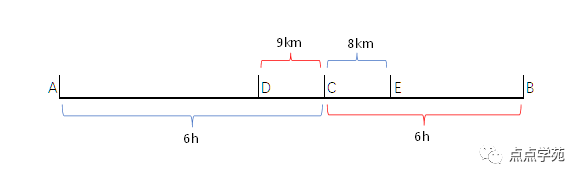
设甲的速度为，乙的速度为，那么，按照常规的方法，可以列出方程组：

看起来妥妥的就是二元二次方程组，这可真难办呀。

设，消去，方程组就是：

化简，可以将二次项等消去，可得：

两式相加，消去 ，可得：

从而可得，也就是甲的速度是每小时10公里。

很明显，按着常规的路程问题列出的方程组太复杂了，不适合小学生。我们需要再深入思考下，简化下方程。

我们考虑下乙提速后的行程问题。

乙提速后比原来多走了9公里，那就说明甲少走了的时间，也就是甲乙两人相遇时少花了这么多时间。

如果按照新的速度，乙在6个小时内会多走公里，但事实上少走了公里。

那就说明乙在的时间里可以走9公里，乙提速后的速度和甲相同。

因此，有：

我们再考虑下甲提速后的行程问题。

甲提速后比原来多走了8公里，那就说明乙少走了的时间，也就是甲乙两人相遇时少花的时间。

如果按照新的速度，甲在6小时内会夺走公里，但事实上少走了公里。

那就说明甲在这段少走的时间里，按照的速度应该要走16公里。

因此，有：

因此，有：

将(1)代入(2)，可以解得，。

因此，甲原来的速度就是每小时10公里。

微信公众号搜索： 北京小学学习资料     家长升学指南  关注公众号，获取最新资讯！

扫码添加“家长论坛”微信好友（微信号 16619908263）

获取YMO世界青少年奥林匹克数学竞赛选拔赛决赛试卷真题
咨询YMO世界青少年奥林匹克数学竞赛政策请拨打电话 16619908263 （同微信号）