[数学]第30届YMO交流活动小学6年级初赛试题

点击领取>>>YMO世界青少年奥林匹克数学竞赛选拔赛决赛试卷题

1、计算：

求s=(      )。

「答案解析」

首先，我们先来算大分数的分子项。

然后我们再来看大分数的分母项。

所以，。

如此这样，我们也可总结出公式：

2、计算：

求s=(      )。

「答案解析」

先统一成假分数，再分类，分别提取公因式。

3、计算：

求s=(      )。

「答案解析」

仔细分析，我们按分母先归类。

4、按规律写出一列算式：，如果要保证被减数比减数大，最多能写出（      ）个算式？

「答案解析」

仔细观察，被减数依次减少7，减数依次增加3。

假设x次后满足要求，那第x次的被减数就是，减数就是，则有如下不等式成立：

可以解得。

由于x只能是整数，那么只能让，此时的算式就是。

所以，最多能写出100个算式。

5、从36到100这65个自然数的乘积的末尾有（  ）个连续的0。

「答案解析」

要求末尾有多少个连续的0，就是要求这段乘积里能分解出多少个2x5，很明显，2的数量肯定比5多，实际上就是求这段乘积里包含多少个5。

因此，末尾有连续16个0。

6、用7个1x2的长方形纸片覆盖一个2x7的方格表，共有（  ）种覆盖方法。

「答案解析」

这样的题目看起来是不是很眼熟呢？

和我们以前做过的题目是不是似曾相识？

其实呀，这个2x7的方格表，我们可以将其看作7级的台阶，1x2的纸片，相当于允许我们一次走一步或两步。

很眼熟了吧，这个其实就是斐波拉契数列，我们可以用倒推法、递归法来解决。

其中，，因此，种。

其实也可不必像上面那么计算，只要将数列写出来，数到第七个便是。

7、观察按下列规律排成的一列数：

在这个数列中，从左边起第m个数记为，当时，m=(     )。

「答案解析」

仔细观察，只要能找到合适的分组方式即可，不需要找到通项公式。

第一组：共1项，分母为，分子为，分子分母和为2。

第二组：共2项，分母依次为，分子依次为，分子分母和为3。

第三组：共3项，分母依次为，分子依次为为，分子分母和为4。

第四组：共4项，分母依次为，分子依次为为，分子分母和为5。

依次类推，既然时，其必定归来在第组。

那么，前面2001组的项数就是：

同时，又在第2002组第二项，因此，。

8、在中选出7个互不相同的数字填入下面的圆圈中，使得每条线段两个端点处所填的数，上面的比下面的大，一共有(    )种填法。

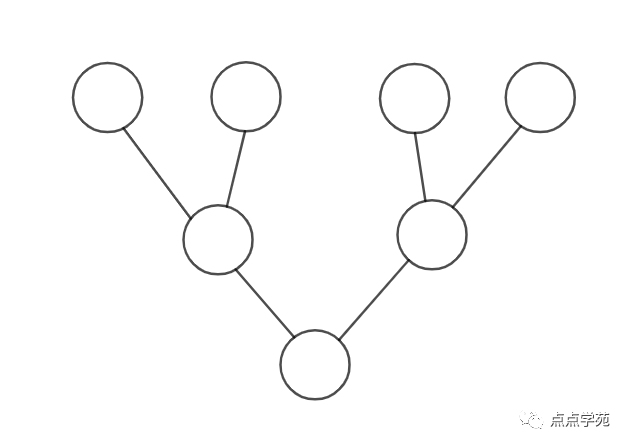
「答案解析」

此类排列组合题目有点难度，题目有一些限制条件要考虑清楚，不然很难做对。

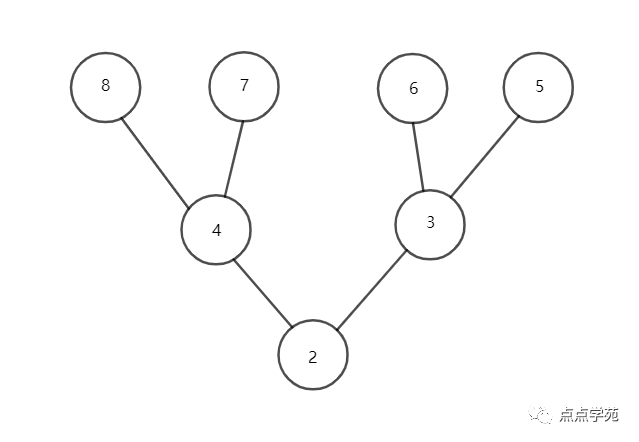
如果我们从这8个数里挑了最小的7个数，那么2只能填最下方，其他6个数随便分成两组，那么无论是在2左边或右边的3个圈里，都可以找到一种合适的填法。

像在上面的例子中，左边我依次填了4、7和8，右边依次填了3、5和6。可以看到，在种组合里，3和4可以互换位置，8,7和6,5也可以互换位置。

什么意思呢，我们固定住最下面的2，从7个数字里任选6个。然后从这6个里任选3个填在左边或右边，剩下的3个填另一边，加上中级层和最上层左边和右边可以互换位置。

因此，这种排法就有种排法。

如果不选择2，那么最下方就只能填3，最上方就只能从剩下的6个里选择，填法就有种。

那么总共就有种。

9、是（   ）的平方。

「答案解析」

注意，，此类阶梯数都有类似规律，中间最大的数字是6，则该阶梯数是6个1的平方。

同时，，

所以，该数是的平方数。

10、六位数能被396整除，这个六位数是（     ）。

「答案解析」

我们先将396分解质因数，很明显，根据被9和11整除的特征，有如下关系：

也就是：

由于和都是0-9的数字，所以，。

因此，有或者，或者，

由于奇偶性相同，因此有两组方程：

很明显，(2)中的，不符合要求。

所以，从(1)中可解得。

因此，这个六位数是207108。

当然了，由于可以将396分解成，由于，我们可以充分利用这一点性质。

由于这个六位数的末两位能被4整除，那么这个六位数必须能被99整除，而：

由于a<10,b<10，因此，必有。

11、，要使这个连乘积的最后5个数字都是0，那么最小的a=（     ）。

「答案解析」

这和前面第5题一样，考查的是乘积中含有多少。

先分解质因数。

很明显，前面的算式中已经包含了4个，还差1个。

所以，最小的a就是10。

12、在2022后面写出三个数字，使所得的七位数被8、9、11整除，那么这三个数字的和是（      ）。

「答案解析」

这和第10题类似，考查的是整除的特征。

设这个七位数的百位数为b，十位数为s，个位数为g。很明显，这三个数字都比10小。

根据被3和9整除的特征，我们有：

可以看出被3整除，被9除余3，那么只能有：

所以，三个数字的和只能是3、12、21。

根据被11整除的特征，我们有：

也就是：

可以看出：

我们就以此为突破口，我们将看作一个整体，根据同奇同偶的关系，（1)和(2)只能列出三组方程组：

同时，根据被2、4、8整除的特征，我们可以得知g是偶数。同时有：

对于方程组(I)，可以解得，很明显，无法满足(2)式。

对于方程组(II)，可以解得，结合(3)，可得，满足(2)式。

对于方程组(III)，可以解得，舍去。

那么，这三个数字的和就是。

这种方法有点复杂，小学生比较难以掌握，有没有更简单一点的方法呢？

由于未知的三个数字全集中在末尾，而

那么，必有，因此，。

因此，三位数的和就是。

13、有一本书有8章，现要求小明每天最少读1章，最多读4章，且必须是整数章。那么他读完这本书一共可以有（  ）种不同的读法。

「答案解析」

此类题目适合用倒推法，运用递归的思路来解决。

我们先考虑最后一天的读法，假设我们将读完第n章的读法记作。

那么，

最后一天读一章，就有种读法，

最后一天读两章，就有种读法，

最后一天读三章，就有种读法，

最后一天读四章，就有种读法，

那么，综合起来，就有如下关系：

依次递归：

然后，我们依次可以计算出，

每天最多读一章只有一种读法，因此。

每天最多读两章有两种读法，因此。

每天最多读三章有四种读法，因此。

每天最多读四章有八种读法，其实也是，因此。

所以：

种读法。

其实，类似的递推公式就是：

完毕。

14、如图，阴影圆环的面积是157平方厘米，那么图中大正方形的面积是（    ）平方厘米。

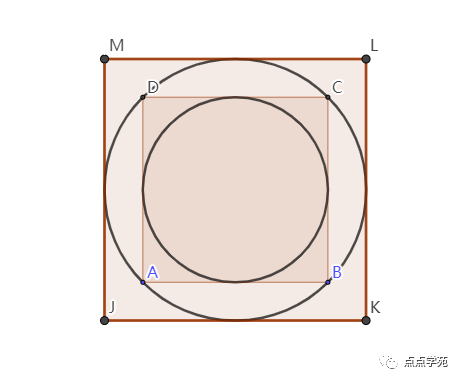
「答案解析」

设大圆的半径为R，小圆的半径为r，因此，圆环的面积就是：

可以得到：

同时，正方形ABCD的面积有两种求法，一种是根据小圆的半径，另外一种就是根据大圆的半径：

因此，，

所以，，所以，大正方形的面积就是。

15、已知自然数满足：除以得到一个完全平方数，则的最小值是（    ）。

「答案解析」

可以依次求出每个质数包含的次数。

(1)计算2出现的次数

(2)计算3出现的次数

(3)计算5出现的次数

(4)计算7出现的次数

(5)计算11出现的次数

(6)计算13出现的次数

因此，的阶乘可写成：

因此，最小的。

由于数字不多，我们可以依次分解质因数，然后将乘积组合起来。

譬如：

再依次补上2,3,5,7,11,13这几个质数各一次，也可以将阶乘分解出来。

16、一个四位数，每一位数字都是1,2,3或4，各个数位上的数字和为12，这样的四位数一共有（  ）个。

「答案解析」

用分类汇总的方法，幸好类别不是太多。

各位数字之和是12，那么只能有如下四种排法：

（1）1,3,4,4的排列有种。

（2）2,2,4,4的排列有种。

（3）2,3,3,4的排列有种。

（4）3,3,3,3的排列只有1种。

一共有种。

17、图中圆环的面积是157平方厘米，那么阴影部分的面积是（   ）平方厘米。

「答案解析」

这和14题一样，设大圆半径为R，小圆半径为r，则可求得：

阴影部分的面积就是：

所以，所求阴影部分面积就是平方厘米。

18、图中是一个钟表的圆面，如果阴影甲的面积是314平方厘米（平行线和圆所夹部分），那么阴影乙的面积是（   ）平方厘米。

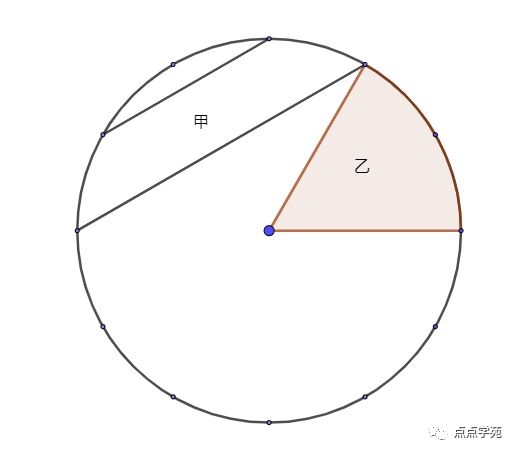
「答案解析」

做下辅助线。

几何图形不好描述，根据一半原理，，同时，圆弧BF段和圆弧AG段的面积相等。

因此，弧乙。

同时，，所以大扇形是小扇形的两倍，有 扇乙，

而,

因此，甲乙。

所以乙的面积就等于甲的面积，也就是平方厘米。

19、现有11块糖，如果小明每天吃奇数块糖，直到吃完，那么小明共有(    )种吃法。

「答案解析」

小学排列组合题，不明白就分类汇总。

所以，总共有种。

这种方式分类多了点，不大友好。

当然，也可以选择其他分类少的方法，分类方式并不是唯一的，简便的方法可以减少计算量和失误。

20、骰子的六个面上是1-6的六个数字，连续掷一枚骰子4次，4次点数之和为10的不同抛掷结果有（  ）种。

「答案解析」

此题和上一题类似，也可以用分类汇总的方法来解决。

我们可以按一定的规律列出所有的组合：

第一种为啥是呢，我们可以将四个位全看作1，然后挑2个位置用2和`6去替换，由于没有顺序，就是排列。也可以先全排列再去重，就是。

微信公众号搜索： 北京小学学习资料     家长升学指南  关注公众号，获取最新资讯！

扫码添加“家长论坛”微信好友（微信号 16619908263）

获取YMO世界青少年奥林匹克数学竞赛选拔赛决赛试卷真题
咨询YMO世界青少年奥林匹克数学竞赛政策请拨打电话 16619908263 （同微信号）