[数学]第24届YMO交流活动小学6年级初赛试题

点击领取>>>YMO世界青少年奥林匹克数学竞赛选拔赛决赛试卷题

（1）(     )。

「答案解析」

注意可以简便计算的特殊数字。

上面每项都是可以帮助我们简便计算的数字，大家要记住其特征。

(2)（     ）。

「答案解析」

注意观察可以简算的数字。

这不科学啊。

(3)(      )。

「答案解析」

这很不科学，看不出有什么规律。

完毕。

(4)(      )。

「答案解析」

先将分数全转换成真分数，注意到分母相同。

(5)(      )。

「答案解析」

首先，119不是质数，由于，能够被7整除。但分解后发现也不能约分，只能老老实实算。

完毕。

(6)(      )。

「答案解析」

先化成真分数。

完毕。

(7)(      )。

「答案解析」

先提取公因式。

完毕。

(8)(      )。

「答案解析」

此类算式千万不能先通分。

完毕。

(9)

「答案解析」

按道理，此类也不要通分。

注意到分子里每小项的分子刚好比其分母的3倍多6，

我们先令，那么：

完毕。

(10)(      )。

「答案解析」

完毕。

(11)(      )。

「答案解析」

完毕。

(12)(      )。

「答案解析」

完毕。

(13)(      )。

「答案解析」

令，那么

所以，。

(14)(      )。

「答案解析」

这个似乎没有什么规律，是不是只能死算呢？

完毕。

(15)(      )。

「答案解析」

完毕。

1、是（   ）的平方。

「答案解析」

像台阶一样逐渐升高，从1升到6，然后再降到1，这样的数叫阶梯数，共有6级台阶，那么它就是6个1的平方，也就是。

同时，。

所以，该数是。

2、已知都是质数，那么(    )。

「答案解析」

由于每个质数除以6的余数，不是1就是2。

如果，那么是3的倍数，那么。

那么，也就是：

都是质数。

仔细观察，当时，此时都满足要求。

那还有其他解吗？

我们只要任取一个k，只要上面5个数中有一个是合数，就说明这样的k不满足要求。

仔细观察，由于第一个数是，和5有关，那么，我们就按5来对k分类好了。

当时，只要，那么是5的倍数，则这样的数不是质数。

当时，也是5的倍数。

当时，也是5的倍数。

当时，也是5的倍数。

当时，也是5的倍数。

所以，只要，无论取什么数，上面5个数中必有一个是5的倍数。

综上所述，是唯一解。

3、一辆车从甲地开往乙地，如果车速提高20%，那么可以比原定时间提前1小时到达。如果以原速行驶90千米后再将车速提高30%，那么也比原定时间提前1小时到达。甲乙两地的距离是(   )公里。

「答案解析」

提速20%，耗时就是原来的，后来提前1小时到达，那么原来的行驶时间就是6小时。

那如果提速30%行驶完全程，需要的时间就是小时，节省的时间就是

事实上只节约了1小时，那么这里差了小时。

也就是说，如果前面90公里也提速30%，那么是可以节省小时的。

那么，原速行驶90公里花的时间就是

那原来的速度就是

那么，甲乙两地的距离就是：

完毕。

4、在一圆形跑道上，甲从A点，乙从B点同时出发反向而行，6分钟后两人相遇，再过4分钟甲到达B点，又过8分钟两人再次相遇，乙环行一周需要（   ）分钟。

「答案解析」

甲走4分钟的路程，乙需要走6分钟，说明甲的速度是乙的倍。

同时，甲乙第一次相遇后反向而行，两人的速度和就是乙的倍，

由于分钟后再次相遇，那么，乙的速度也是12分钟的2.5倍。

因此，乙环行一周需要的时间就是分钟。

5、如图，三角形ABC中BC边的高AD长7厘米，三角形BCE中BC边的高EF长4厘米，并且已知，则(      )平方厘米。

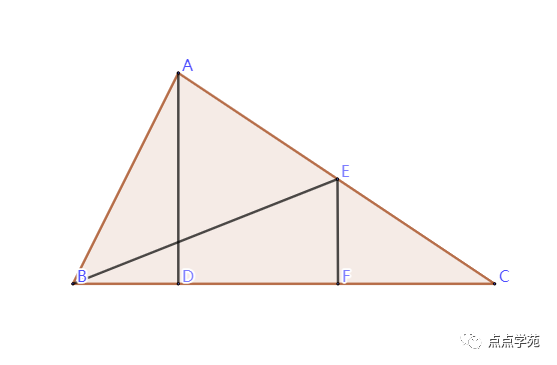
「答案解析」

同底三角形面积之比等于高之比。

所以，平方厘米。

6、如图，面积为36平方厘米的正方形ABCD中，E、F是DC边上的三等分点，那么阴影部分的面积是（    ）平方厘米。

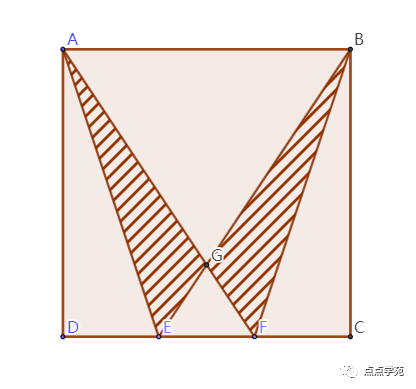
「答案解析」

依题意，，

因此，。

所以，阴影部分的面积就是平方厘米。

7、如下图，正方形ABCD中，E为AD的中点，，求的值是（     ）。

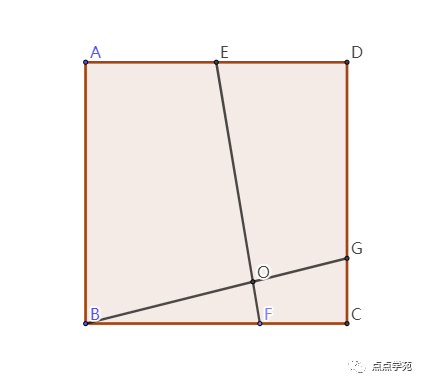
「答案解析」

如图所示，做上一些辅助线。

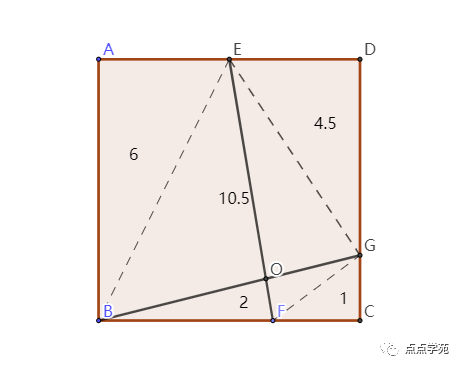
假设，

根据题目里的比例关系，那么，正方形面积就是。

那么，,

。

同理，，

因此，。

8、如图所示，在中，，D是AE的中点，那么(      )。

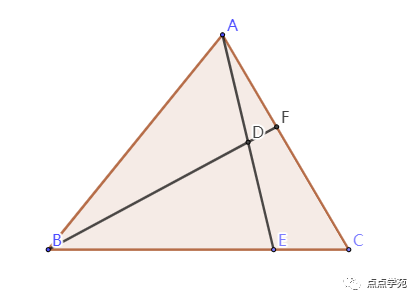
「答案解析」

如下图，连上CD。

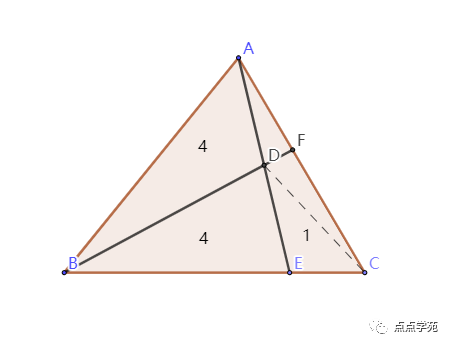
假设，那么，。

因此，。

9、甲乙两个工程队分别负责两项工程。晴天，甲完成工程需要10天，乙完成工程需要16天。雨天，甲和乙的工作效率分别是晴天时的30%和80%。实际情况时两队同时开工，同时完工。那么在施工期间，下雨的天数时（    ）天。

「答案解析」

假设下雨天数是天，晴天是天。

则有：

可以解得。

同时，

可以解得，

因此，天。

10、一个十位数，如果各位上的数字都不相同，那么就称为"十全数"，例如，3785942160就是一个十全数。现已知一个十全数能被整除，并且它的前四位数十4876，那么这个十全数是（        ）。

「答案解析」

由于该数能同时被2和5整除，所以末位数必定是0。

同时，该数也能被4整除，那么末两位数必定能被4整除，那么，末两位数必定是20。

设该数是，那未知的四个数只能在中选择。

同时，由于能被9和11整除，那么该数必定能被99整除，而。

因此，

所以

由于

所以

此时

同时，该数能被7、11、13整除，那么必定能被1001整除，那么，必有：

由于a只能是3或1，d只能是9和5，那么，只能有这样的关系：

也就是：

那么，只能推论出如下关系：

那么，所求的数可能就是。

很明显，这个数的末三位能被8整除，那么该数也能被8整除。末四位能被16整除，该数能被16整除。

综合起来，该数已经能被整除，满足要求。

11、记，这里，当k在1至2019之间取正整数值时，有（   ）个不同的k，使得s是一个正整数的平方。

「答案解析」

很明显，任何偶数的平方都是4的倍数，任何奇数的平方可以写成：

的形式，也就是说，任何奇数的平方被4除余1。

而在中，只要，那么必定是4的倍数，那么，那么永远不可能是平方数。

因此，。

所以，。

因此，，

也就是，在从到奇数的平方中，满足条件的刚好有个。

微信公众号搜索： 北京小学学习资料     家长升学指南  关注公众号，获取最新资讯！

扫码添加“家长论坛”微信好友（微信号 16619908263）

获取YMO世界青少年奥林匹克数学竞赛选拔赛决赛试卷真题
咨询YMO世界青少年奥林匹克数学竞赛政策请拨打电话 16619908263 （同微信号）