2022年全国高中数学联赛B1卷试题及参考答案

一、填空题：本大题共8小题，每小题10分，满分80分．

1. 若等差数列的各项非零，且，则的值为__________．

2. 在平面直角坐标系中，圆的方程为，则圆的面积为__________．

3. 将一枚质地均匀的骰子连续掷两次，则后一次所得点数不小于前一次所得点数的概率为__________．

4. 设，若，，则的值为__________．

5. 设为复数，集合（为虚数单位）．若的所有元素之和为，则的所有元素之积为__________．

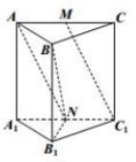
6. 如图，已知正三棱柱的所有棱长都相等，棱,的中点分别为,，则异面直线与所成的角的余弦值为__________．

7. 设实数满足：函数的图像有对称中心，且与函数的图像有公共点，则的取值范围是__________．

8. 有四所学校的学生参加一项数学竞赛，每所学校派出名选手．组委会要抽选其中若干名选手做一项调研，要求任意两所学校被抽中的选手数之和至少为、至多为，则不同的抽选方式数为__________（结果用数值表示）．

二、解答题：本大题共4小题，满分120分．解答应写出文字说明、证明过程或演算步骤．

9. （本题满分20分） 解方程：．

10. （本题满分20分） 在平面直角坐标系中，轴正半轴上的两个动点、满足，抛物线：上一点满足，过点作的切线，记点到直线的距离为．求的最小值，并求出当取到最小值时数量积的值．

11. （本题满分40分） 对任意三个两两不同的非负实数,,，定义并设能取到的最小值为．(1)证明：当,,均为正数时，；(2)求所有非负实数组，使得．

12. （本题满分40分） 对每个正整数，将形如（,,为正整数）的整数称为“-有趣数”．(1)判断是否为-有趣数，说明理由；(2)求所有正整数，使得存在两个-有趣数互为相反数．