点击领取>>>全国高中数学联赛各赛区历届真题试卷及答案

[引言]从2010年起,国内数学高联赛分为一试和二试(加试)。一试考试时间为每年9月中旬第一个周日上午8:00—9:20,共80分钟。包括8道填空题(每题8分)和3道解答题(分别为16分、20分、20分),满分120分。[题目9]若△ABC的内角A,B,C满足sinA=cosB=tanC,求cos3A+cos2A-cosA的值.[解析]由于sinA=cosB,所以A=π/2±B。又由于tanC有意义,所以C不为直角,即只能为A=π/2+B。于是,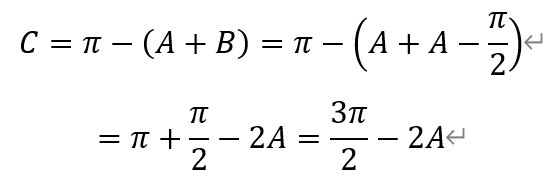
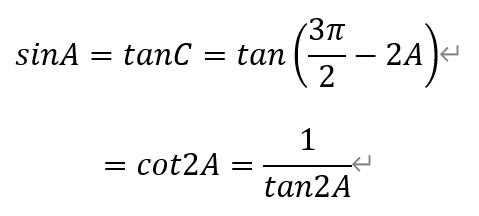
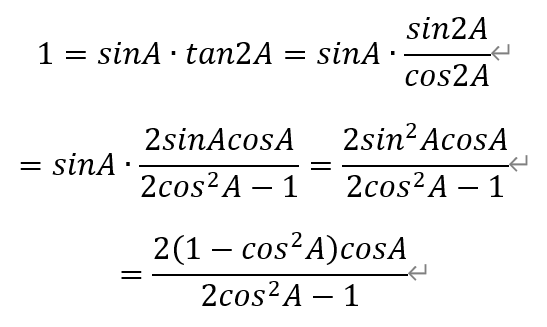
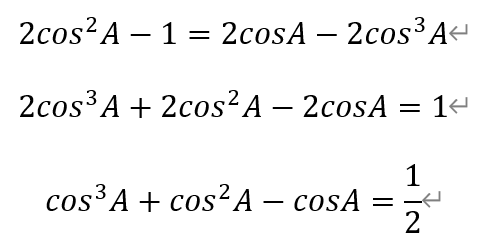
[题目10]给定正整数m(m≥3)。设正项等差数列{an}与正项等比数列{bn}满足:{an}的首项等于{bn}的公比,{bn}的首项等于{an}的公差,且am=bm。求am的最小值,并确定当am取到最小值时a1与b1的比值。[解析]根据题设,设数列{an}的首项为a,公差为b,数列{bn}的首项为b,公差为a,其中,a,b>0。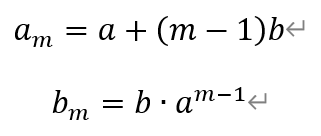
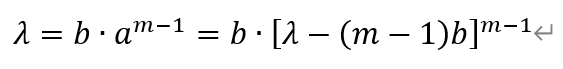
将上式两边乘以(m-1)2,并利用多元均值不等式,有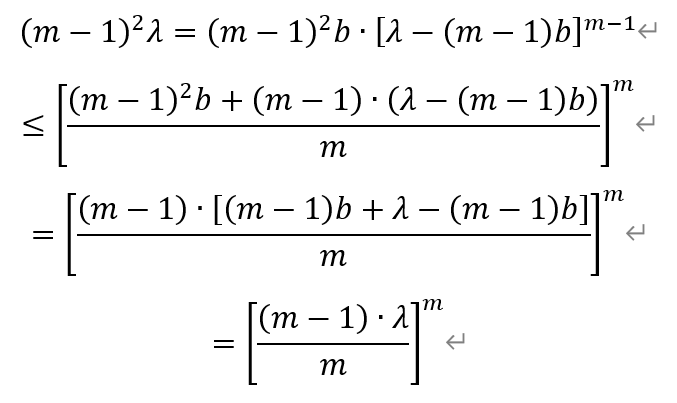
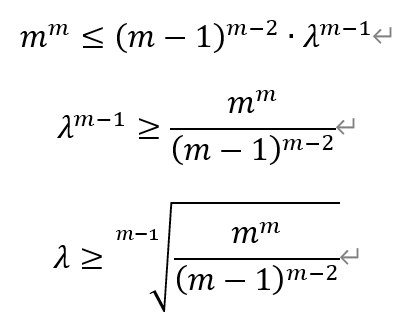
当且仅当(m-1)2b=λ-(m-1)b时取等,即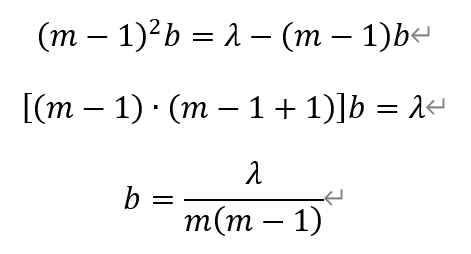
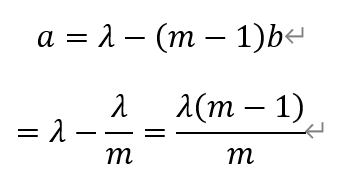
于是,当am取到最小值时,即λ取得最小值时,a1与b1的比值为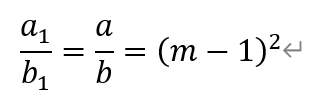
[题目11]在平面直角坐标系中,双曲线Г:x2/3-y2=1。对平面内不在Г上的任意一点P,记ΩP为过点P且与Г有两个交点的直线的全体。对任意直线l∈ΩP,记M,N为l与Г的两个交点,定义fP(l)=|PM|•|PN|。若存在一条直线l0∈ΩP,满足:l0与Г的两个交点位于y轴异侧,且对任意直线l∈ΩP,l≠l0,均有fP(l)>fP(l0),则称P为“好点”。求所有好点所构成的区域的面积。[解析]设P(a,b)为好点,下面求取a,b需满足的充要条件。对任意直线l∈ΩP,设直线l的倾角为θ(0≤θ<π),则直线l的参数方程为,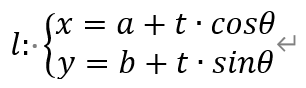
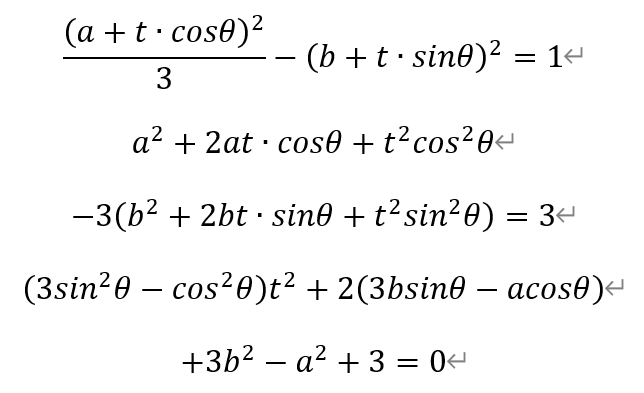
根据题设,上述二次方程有两个不同的解,因此3sin2θ-cos2θ≠0,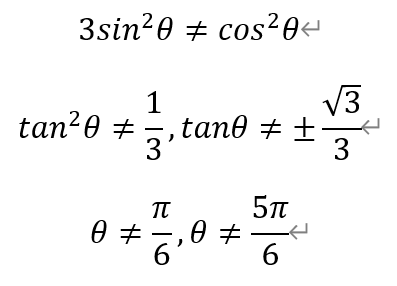
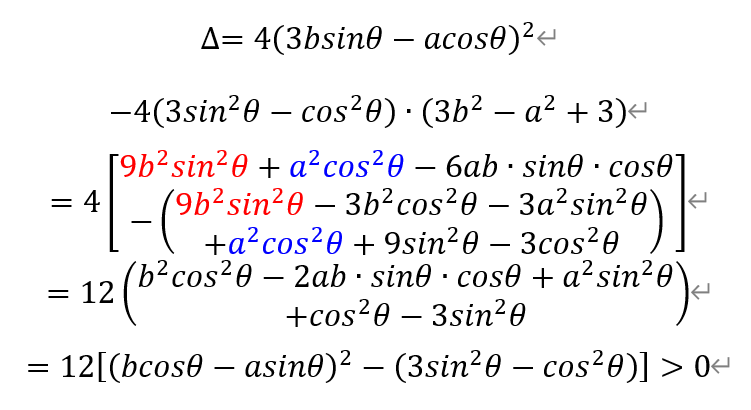
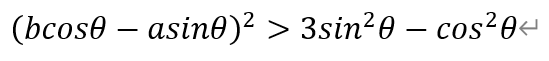
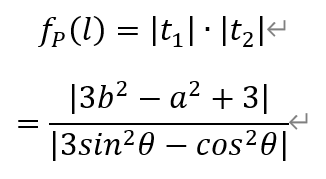
当l与Г交于y轴异侧两点时,由双曲线Г的性质可知θ∈[0,π/6)∪(5π/6,π)。此时3sin2θ-cos2θ<0,于是有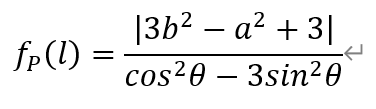
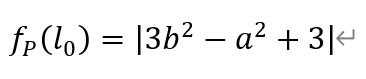
当l与Г交于y轴同侧两点时,由双曲线Г的性质可知θ∈(π/6,5π/6)。若存在符合题意的l,有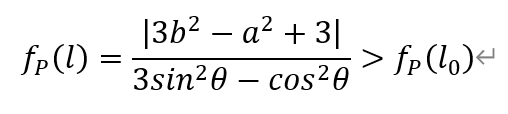
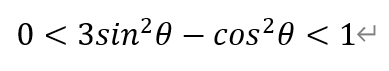
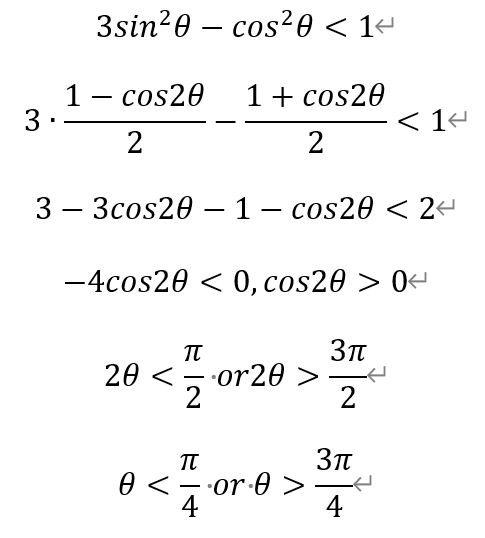
即θ∈(π/6,π/4)∪(3π/4,5π/6)。换句话讲,对于θ∈[π/4,3π/4],a,b不满足前述条件,即
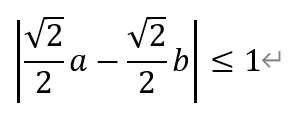
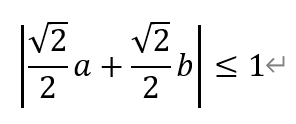
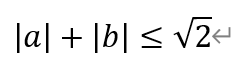
反之,若上式成立,且θ∈[π/4,3π/4],注意到,此时sinθ≥|cosθ≥0,则有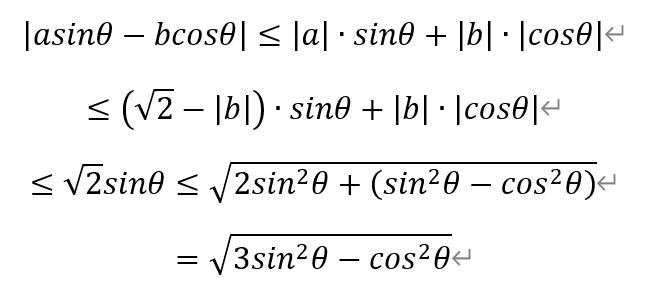
综上,P(a,b)为好点的充分必要条件为|a|+|b|≤√2。所求的面积为4。
微信公众号搜索: 北京小学学习资料 家长升学指南 关注公众号,获取最新资讯!

扫码添加“家长论坛”微信好友(微信号 16619908263)
获取历年全国高中数学联赛各赛区历届真题试卷及答案
咨询全国高中数学联赛政策请拨打电话 16619908263 (同微信号)

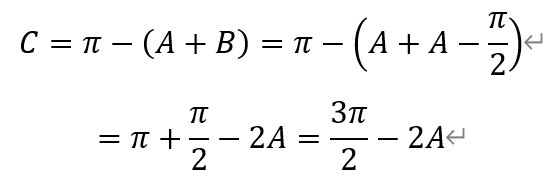
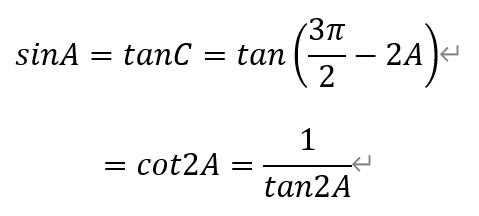
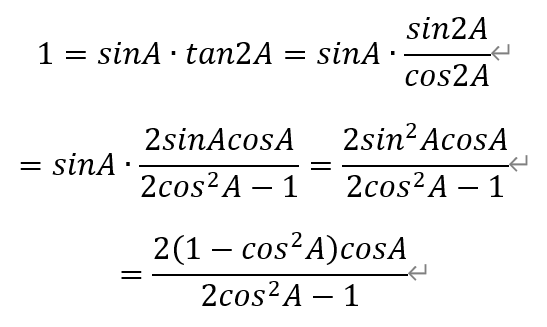
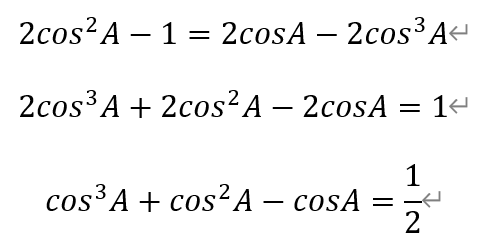
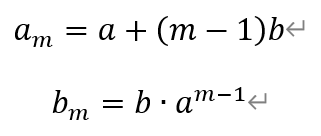
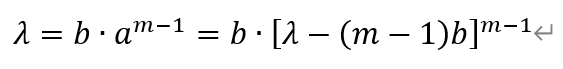
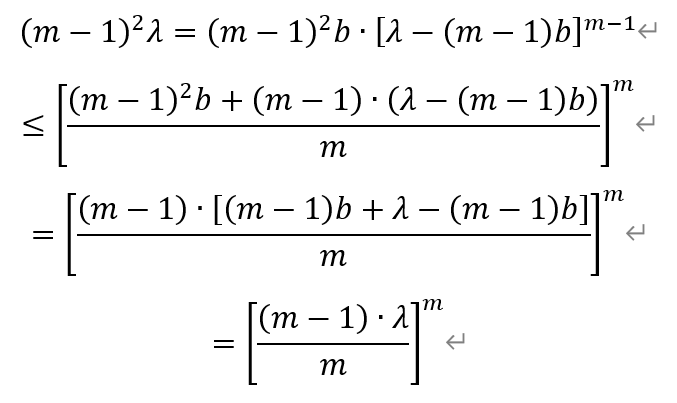
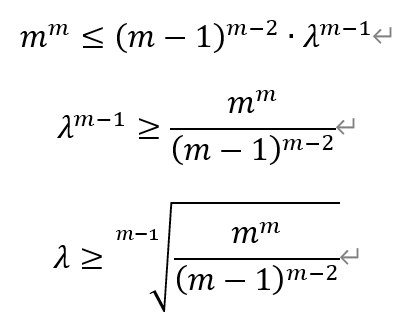
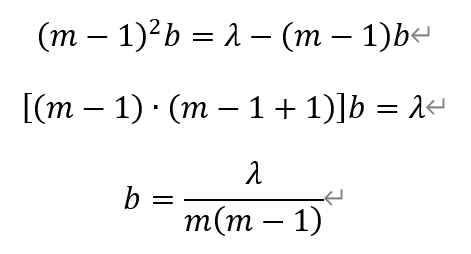
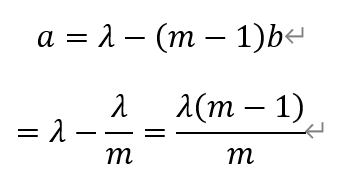
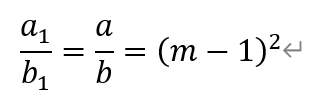
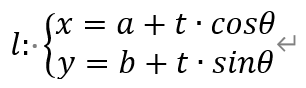
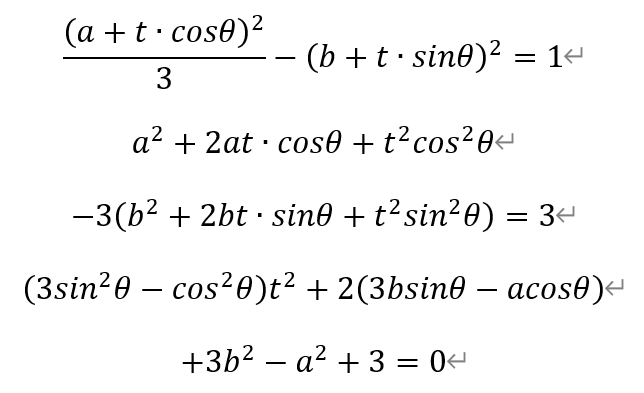
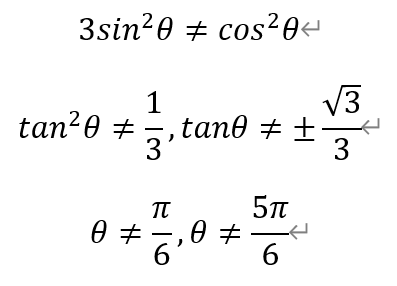
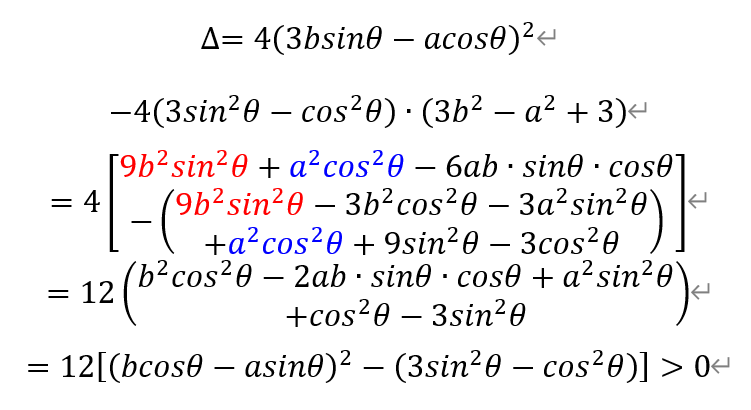
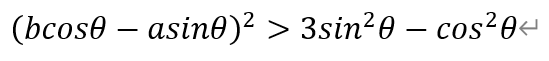
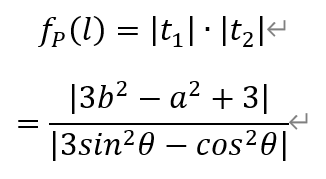
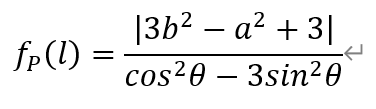
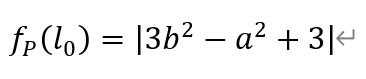
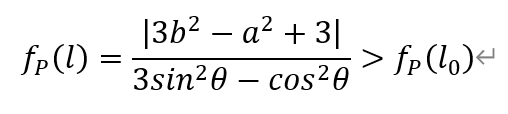
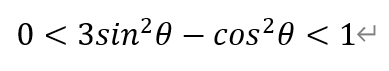
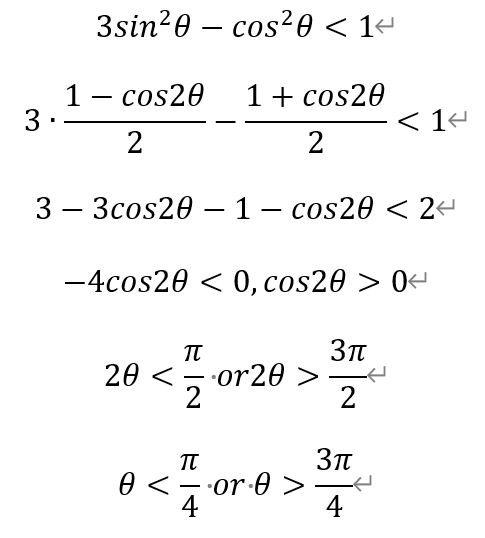

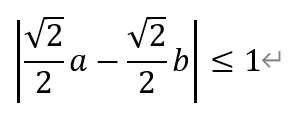
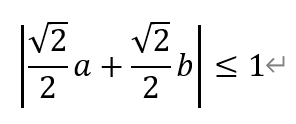
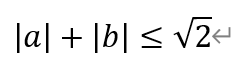
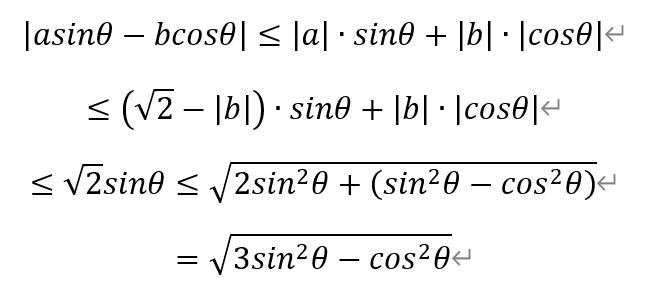


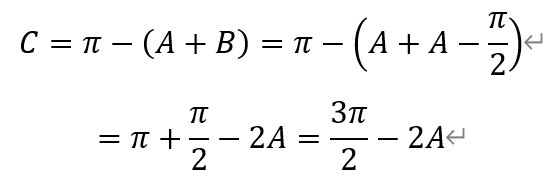
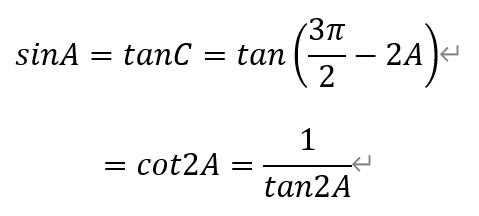
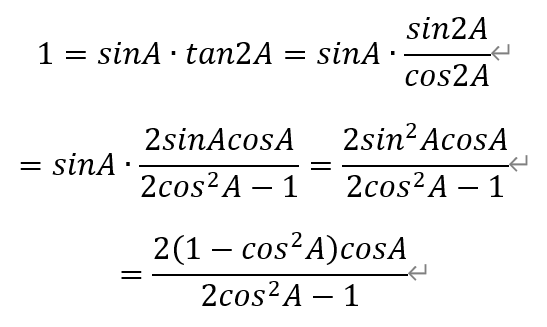
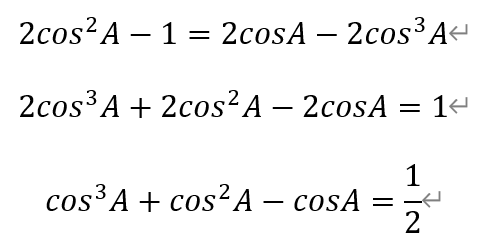
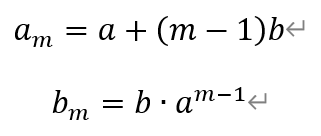
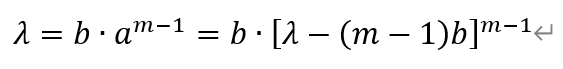
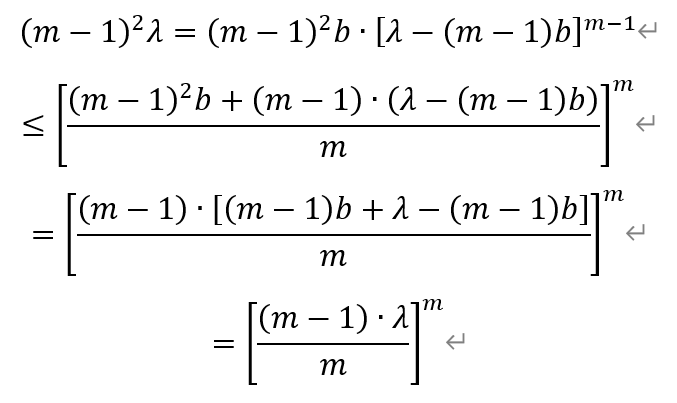
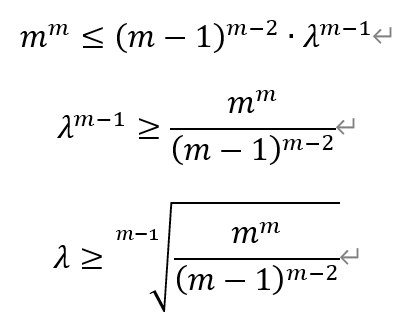
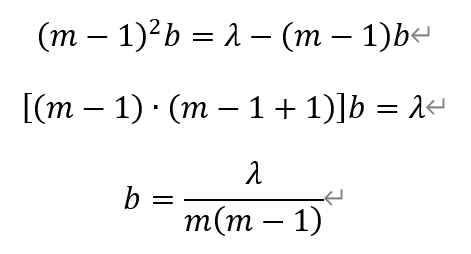
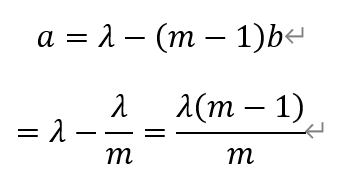
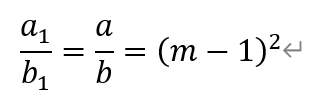
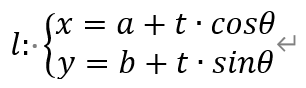
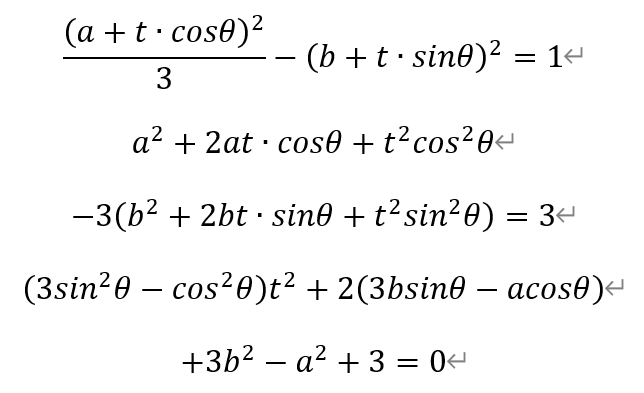
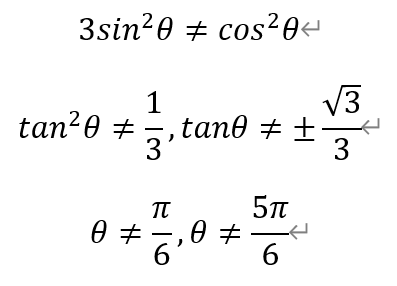
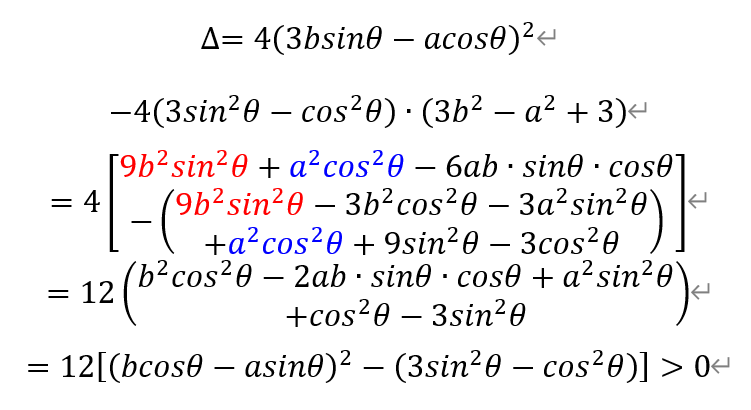
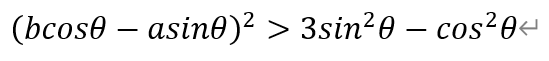
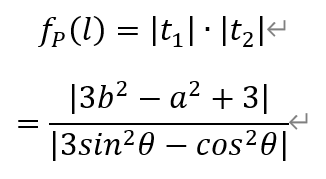
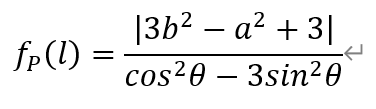
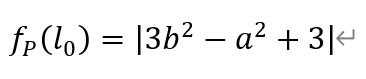
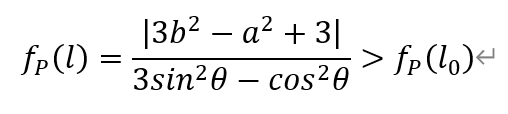
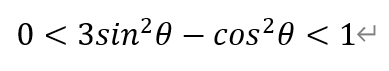
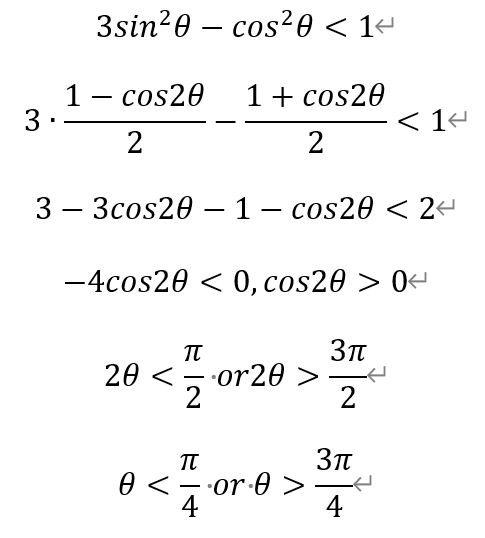

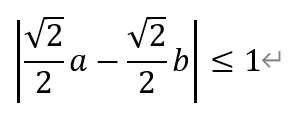
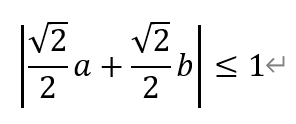
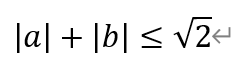
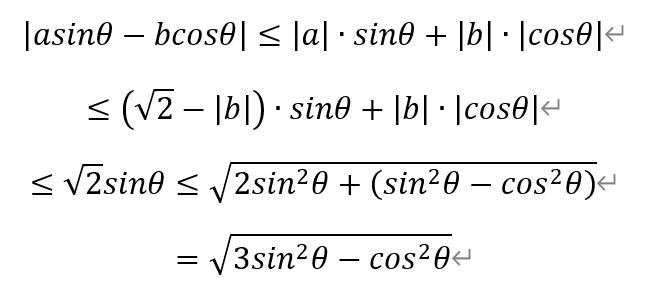

0 个回复